算法解题套路框架

回溯

模板

无论是排列、组合还是子集问题，简单说无非就是让你从序列 nums 中以给定规则取若干元素，主要有以下几种变体：

1.元素无重不可复选，即 nums 中的元素都是唯一的，每个元素最多只能被使用一次，这也是最基本的形式。以组合为例，如果输入 nums = [2,3,6,7]，和为 7 的组合应该只有 [7]。

// 组合/子集问题回溯算法框架 
func backtrack(nums []int, start int) {
    // 回溯算法标准框架 
    for i := start; i < len(nums); i++ {
        // 做选择
        track = append(track, nums[i])
        // 注意参数 
        backtrack(nums, i+1)
        // 撤销选择 
        track = track[:len(track)-1]
    }
}

// 排列问题回溯算法框架
func backtrack(nums []int) {
    for i := 0; i < len(nums); i++ {
        // 剪枝逻辑 
        if used[i] {
            continue
        }
        // 做选择 
        used[i] = true
        track = append(track, nums[i])

        backtrack(nums)
        // 撤销选择 
        track = track[:len(track)-1]
        used[i] = false
    }
}

2.元素可重不可复选，即 nums 中的元素可以存在重复，每个元素最多只能被使用一次。以组合为例，如果输入 nums = [2,5,2,1,2]，和为 7 的组合应该有两种 [2,2,2,1] 和 [5,2]。

sort.Ints(nums)
// 组合/子集问题回溯算法框架
func backtrack(nums []int, start int) {
    // 回溯算法标准框架
    for i := start; i < len(nums); i++ {
        // 剪枝逻辑，跳过值相同的相邻树枝
        if i > start && nums[i] == nums[i-1] {
            continue
        }
        // 做选择
        track = append(track, nums[i])
        // 注意参数
        backtrack(nums, i+1)
        // 撤销选择
        track = track[:len(track)-1]
    }
}


sort.Ints(nums)
// 排列问题回溯算法框架
func backtrack(nums []int) {
    for i := 0; i < len(nums); i++ {
        // 剪枝逻辑
        if used[i] {
            continue
        }
        // 剪枝逻辑，固定相同的元素在排列中的相对位置
        if i > 0 && nums[i] == nums[i-1] && !used[i-1] {
            continue
        }
        // 做选择
        used[i] = true
        track = append(track, nums[i])

        backtrack(nums)

        // 撤销选择
        track = track[:len(track)-1]
        used[i] = false
    }
}

3.元素无重可复选，即 nums 中的元素都是唯一的，每个元素可以被使用若干次。以组合为例，如果输入 nums = [2,3,6,7]，和为 7 的组合应该有两种 [2,2,3] 和 [7]。

// 组合/子集问题回溯算法框架
func backtrack(nums []int, start int) {
    // 回溯算法标准框架
    for i := start; i < len(nums); i++ {
        // 做选择
        track = append(track, nums[i])
        // 注意参数
        backtrack(nums, i)
        // 撤销选择
        track = track[:len(track)-1]
    }
}

// 排列问题回溯算法框架
func backtrack(nums []int) {
    for i := 0; i < len(nums); i++ {
        // 做选择
        track = append(track, nums[i])
        backtrack(nums)
        // 撤销选择
        track = track[:len(track)-1]
    }
}

例题

LeetCode	难度	类型
78.子集	🟠	子集（元素无重不可复选）
77.组合	🟠	组合（元素无重不可复选）
216.组合总和 III	🟠	组合（元素无重不可复选）
46.全排列	🟠	排列（元素无重不可复选）
90.子集 II	🟠	子集（元素可重不可复选）
40.组合总和 II	🟠	组合（元素可重不可复选）
47.全排列 II	🟠	排列（元素可重不可复选）
39.组合总和	🟠	组合（元素无重可复选）
22. 括号生成	🟠
698. 划分为k个相等的子集	🟠

78.子集（元素无重不可复选）

给你一个整数数组 nums ，数组中的元素互不相同。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按任意顺序返回解集。

示例 1：

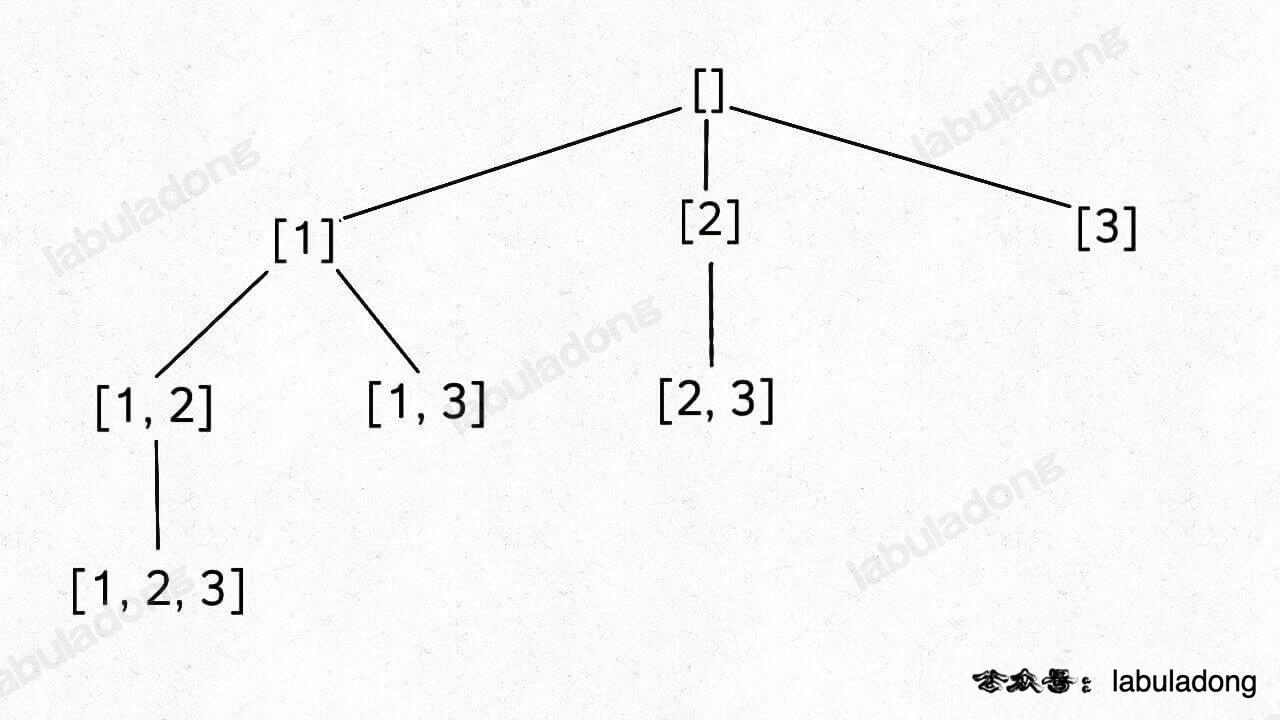
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

我们使用 start 参数控制树枝的生长避免产生重复的子集，用 track 记录根节点到每个节点的路径的值，同时在前序位置把每个节点的路径值收集起来，完成回溯树的遍历就收集了所有子集。

func subsets(nums []int) [][]int {
    var res [][]int
    // 记录回溯算法的递归路径
    var track []int
    
    // 回溯算法核心函数，遍历子集问题的回溯树
    var backtrack func(int)
    backtrack = func(start int) {
        // 前序位置，每个节点的值都是一个子集
        res = append(res, append([]int(nil), track...))
        
        // 回溯算法标准框架
        for i := start; i < len(nums); i++ {
            // 做选择
            track = append(track, nums[i])
            // 通过 start 参数控制树枝的遍历，避免产生重复的子集
            backtrack(i + 1)
            // 撤销选择
            track = track[:len(track)-1]
        }
    }

    backtrack(0)
    return res
}

77.组合（元素无重不可复选）

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按任何顺序返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

这是标准的组合问题，但我给你翻译一下就变成子集问题了：

给你输入一个数组 nums = [1,2..,n] 和一个正整数 k，请你生成所有大小为 k 的子集。

还是以 nums = [1,2,3] 为例，刚才让你求所有子集，就是把所有节点的值都收集起来；现在你只需要把第 2 层（根节点视为第 0 层）的节点收集起来，就是大小为 2 的所有组合：

反映到代码上，只需要稍改 base case，控制算法仅仅收集第 k 层节点的值即可：

func combine(n int, k int) [][]int {
    var res [][]int
    // 记录回溯算法的递归路径
    var track []int

    // 回溯算法核心函数
    var backtrack func(int)
    backtrack = func(start int) {
        // base case
        if k == len(track) {
            // 遍历到了第 k 层，收集当前节点的值
            res = append(res, append([]int(nil), track...))
            return
        }

        // 回溯算法标准框架
        for i := start; i <= n; i++ {
            // 选择
            track = append(track, i)
            // 通过 start 参数控制树枝的遍历，避免产生重复的子集
            backtrack(i + 1)
            // 撤销选择
            track = track[:len(track)-1]
        }
    }

    backtrack(1)
    return res
}

216.组合总和 III（元素无重不可复选）

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

只使用数字 1 到 9
每个数字最多使用一次

返回所有可能的有效组合的列表。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

func combinationSum3(k int, n int) [][]int {
	var res [][]int
	var track []int
	var trackSum int

	var backtrack func(int)
	backtrack = func(start int) {
        // 当满足条件时，收集 track 的值
		if k == len(track) && trackSum == n {
			res = append(res, append([]int(nil), track...))
		}

		if trackSum > n || len(track) > k {
			return
		}

        // 从 start 开始遍历到 9（只能使用数字 1-9）
		for i := start; i <= 9; i++ {
			trackSum += i
			track = append(track, i)
			backtrack(i + 1)
			track = track[:len(track)-1]
			trackSum -= i
		}
	}

	backtrack(1)
	return res
}

46.全排列（元素无重不可复选）

给定一个不含重复数字的数组 nums ，返回其所有可能的全排列。你可以按任意顺序返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

刚才讲的组合/子集问题使用 start 变量保证元素 nums[start] 之后只会出现 nums[start+1..] 中的元素，通过固定元素的相对位置保证不出现重复的子集。

但排列问题本身就是让你穷举元素的位置，nums[i] 之后也可以出现 nums[i] 左边的元素，所以之前的那一套玩不转了，需要额外使用 used 数组来标记哪些元素还可以被选择。

标准全排列可以抽象成如下这棵多叉树：

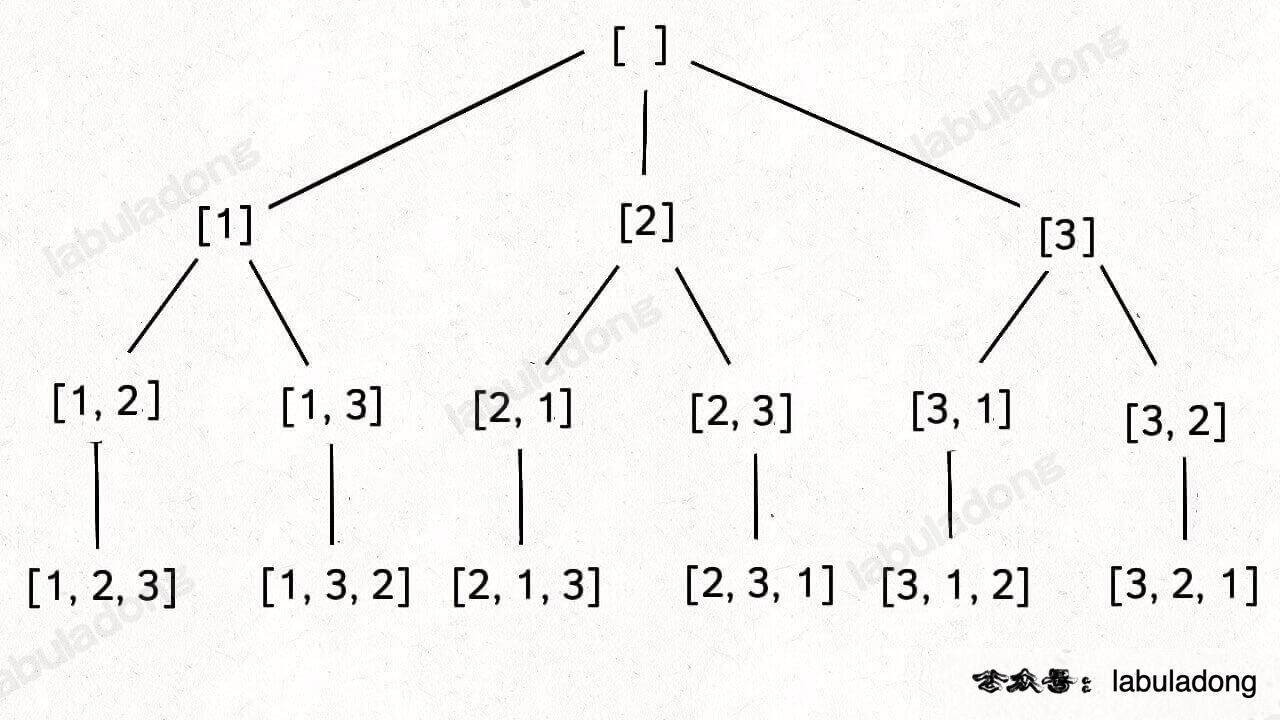
我们用 used 数组标记已经在路径上的元素避免重复选择，然后收集所有叶子节点上的值，就是所有全排列的结果：

func permute(nums []int) [][]int {
    var res [][]int
    // 记录回溯算法的递归路径
    var track []int
    // track 中的元素会被标记为 true
    used := make([]bool, len(nums))

    // 回溯算法核心函数
    var backtrace func()
    backtrace = func() {
        // base case，到达叶子节点
        if len(track) == len(nums) {
            // 收集叶子节点上的值
            res = append(res, append([]int(nil), track...))
            return
        }
        // 回溯算法标准框架
        for i := 0; i < len(nums); i++ {
            if used[i] {
                continue
            }
            // 做选择
            used[i] = true
            track = append(track, nums[i])
            // 进入下一层回溯树
            backtrace()
            // 取消选择
            track = track[:len(track)-1]
            used[i] = false
        }
    }
    backtrace()
    return res
}

90.子集 II（元素可重不可复选）

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。返回的解集中，子集可以按任意顺序排列。

示例 1：

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

需要进行剪枝去除重复结果，如果一个节点有多条值相同的树枝相邻，则只遍历第一条，剩下的都剪掉，不要去遍历。

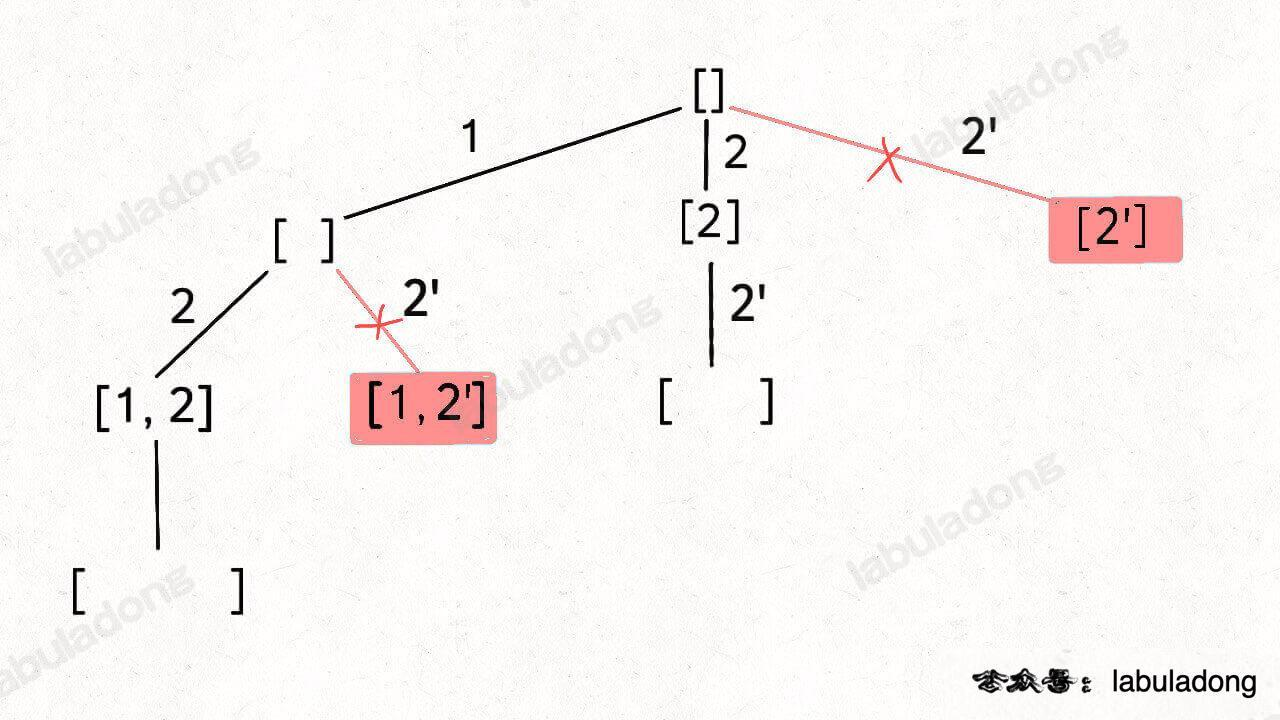
先对元素进行排序，让相同的元素靠在一起，如果发现 nums[i] == nums[i-1]，则跳过：

func subsetsWithDup(nums []int) [][]int {
	var res [][]int
    // 记录回溯算法的递归路径
	var track []int
    // 先排序，让相同的元素靠在一起
	sort.Ints(nums)

	var backtrack func(int)
	backtrack = func(start int) {
        // 前序位置，每个节点的值都是一个子集
		res = append(res, append([]int(nil), track...))

		for i := start; i < len(nums); i++ {
            // 剪枝逻辑，值相同的相邻树枝，只遍历第一条
			if i > start && nums[i] == nums[i-1] {
				continue
			}
			track = append(track, nums[i])
			backtrack(i + 1)
			track = track[:len(track)-1]
		}
	}
	backtrack(0)
	return res
}

40.组合总和 II（元素可重不可复选）

给定一个候选人编号的集合 candidates 和一个目标数 target，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

注意：解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

说这是一个组合问题，其实换个问法就变成子集问题了：请你计算 candidates 中所有和为 target 的子集。

对比子集问题的解法，只要额外用一个 trackSum 变量记录回溯路径上的元素和，然后将 base case 改一改即可解决这道题：

func combinationSum2(nums []int, target int) [][]int {
	var res [][]int
	var track []int
    // 记录 track 中的元素之和
	var trackSum int
    // 先排序，让相同的元素靠在一起
	sort.Ints(nums)

    // 回溯算法主函数
	var backtrack func(int)
	backtrack = func(start int) {
        // base case，达到目标和，找到符合条件的组合
		if trackSum == target {
			res = append(res, append([]int(nil), track...))
            return
		}
        // base case，超过目标和，直接结束
		if trackSum > target {
			return
		}
        // 回溯算法标准框架
		for i := start; i < len(nums); i++ {
            // 剪枝逻辑，值相同的树枝，只遍历第一条
			if i > start && nums[i] == nums[i-1] {
				continue
			}
            // 做选择
			track = append(track, nums[i])
			trackSum += nums[i]
            // 递归遍历下一层回溯树
			backtrack(i + 1)
            // 撤销选择
			track = track[:len(track)-1]
			trackSum -= nums[i]
		}
	}
	backtrack(0)
	return res
}

47.全排列 II（元素可重不可复选）

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

对比之前的标准全排列解法代码，这段解法代码只有两处不同：

1.对 nums 进行了排序。
2.添加了一句额外的剪枝逻辑。

func permuteUnique(nums []int) [][]int {
	var res [][]int
	var track []int
    // track 中的元素会被标记为 true
	used := make([]bool, len(nums))
    // 先排序，让相同的元素靠在一起
	sort.Ints(nums)

	var backtrack func()
	backtrack = func() {
		if len(track) == len(nums) {
			res = append(res, append([]int(nil), track...))
            return
		}
        // 注意起始是 0，没有 start
		for i := 0; i < len(nums); i++ {
			if used[i] {
				continue
			}
            // 新添加的剪枝逻辑，固定相同的元素在排列中的相对位置
            // 说明当前数字与前一个数字相同，并且前一个数字尚未被使用，此时跳过以避免重复排列
			if i > 0 && nums[i] == nums[i-1] && !used[i-1] {
				continue
			}

			used[i] = true
			track = append(track, nums[i])
			backtrack()
			track = track[:len(track)-1]
			used[i] = false
		}
	}
	backtrack()
	return res
}

39.组合总和（元素无重可复选）

给你一个无重复元素的整数数组 candidates 和一个目标整数 target，找出 candidates 中可以使数字和为目标数 target 的所有不同组合，并以列表形式返回。你可以按任意顺序返回这些合。

candidates 中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

在之前处理无重复元素的子集/组合问题时，我们在调用 backtrack 函数的时候传入 i + 1，这个 i 从 start 开始，那么下一层回溯树就是从 start + 1 开始，从而保证 nums[start] 这个元素不会被重复使用。

那么反过来，如果我想让每个元素被重复使用，我只要把 i + 1 改成 i 即可：

func combinationSum(nums []int, target int) [][]int {
	var res [][]int
    // 记录回溯的路径
	var track []int
    // 记录 track 中的路径和
    var trackSum int

    var backtrack func(int)
    backtrack = func(start int) {
        // base case，找到目标和，记录结果
        if trackSum == target {
            res = append(res, append([]int(nil), track...))
            return
        }
        // base case，超过目标和，停止向下遍历
        if trackSum > target {
            return
        }

        // 回溯算法标准框架
        for i := start; i < len(nums); i++ {
            // 选择 nums[i]
            trackSum += nums[i]
            track = append(track, nums[i])
            // 递归遍历下一层回溯树
            // 同一元素可重复使用，注意参数
            backtrack(i)
            // 撤销选择 nums[i]
            track = track[:len(track)-1]
            trackSum -= nums[i]
        }
    }

    backtrack(0)
    return res

}

22.括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且有效的括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

这道题的核心思路是通过递归回溯生成所有可能的括号组合，并用剪枝条件确保只生成合法的组合：

1. 用 left 和 right 分别表示剩余的左括号和右括号数量。
1. 剪枝条件：右括号数量不能少于左括号（right < left）且括号数量不能小于 0。
1. 每次递归选择添加左括号或右括号，并在左右括号都用完时记录结果。

func generateParenthesis(n int) []string {
    var track string
    var res []string

    var backtrack func(left, right int)
    backtrack = func(left, right int) {
        // 若左括号剩下的多，说明不合法
        // 可以排除掉类似 ))(( 这种无效的括号，因为 ))( 的时候 right < left，已经被排除了
        if right < left {
            return
        }
        // 数量小于 0 肯定是不合法的
        if left < 0 || right < 0 {
            return
        }
        // 当所有括号都恰好用完时，得到一个合法的括号组合
        if left == 0 && right == 0 {
            res = append(res, track)
            return
        }

        // 做选择，尝试放一个左括号
        track += "("
        backtrack(left-1, right)
        // 撤销选择
        track = track[:len(track)-1]

        // 做选择，尝试放一个右括号
        track += ")"
        backtrack(left, right-1)
        // 撤销选择
        track = track[:len(track)-1]
    }

    backtrack(n, n)
    return res
}

698. 划分为k个相等的子集

给定一个整数数组 nums 和一个正整数 k，找出是否有可能把这个数组分成 k 个非空子集，其总和都相等。

示例 1：

输入： nums = [4, 3, 2, 3, 5, 2, 1], k = 4
输出： True
说明： 有可能将其分成 4 个子集（5），（1,4），（2,3），（2,3）等于总和。

数组

快慢指针

原地修改

26. 删除有序数组中的重复项

给你一个非严格递增排列的数组 nums，请你原地删除重复出现的元素，使每个元素只出现一次，返回删除后数组的新长度。元素的相对顺序应该保持一致。然后返回 nums 中唯一元素的个数。

考虑 nums 的唯一元素的数量为 k，你需要做以下事情确保你的题解可以被通过：

更改数组 nums，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k。

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

我们让慢指针 slow 走在后面，快指针 fast 走在前面探路，找到一个不重复的元素就赋值给 slow 并让 slow 前进一步。

这样，就保证了 nums[0..slow] 都是无重复的元素，当 fast 指针遍历完整个数组 nums 后，nums[0..slow] 就是整个数组去重之后的结果。

func removeDuplicates(nums []int) int {
    if len(nums) == 0 {
        return 0
    }
    slow,fast :=0,0
    for fast<len(nums) {
        if nums[fast] != nums[slow] {
            slow++
            // 维护 nums[0..slow] 无重复
            nums[slow] = nums[fast]
        }
        fast++
    }
    // 数组长度为索引 + 1
    return slow + 1
}

27. 移除元素

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。

假设 nums 中不等于 val 的元素数量为 k，要通过此题，您需要执行以下操作：

更改 nums 数组，使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
返回 k。

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2,_,_]
解释：你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。
你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

如果 fast 遇到值为 val 的元素，则直接跳过，否则就赋值给 slow 指针，并让 slow 前进一步。

这和前面说到的数组去重问题解法思路是完全一样的，直接看代码：

func removeElement(nums []int, val int) int {
    fast, slow := 0, 0
    for fast < len(nums) {
        if nums[fast] != val {
            nums[slow] = nums[fast]
            slow++
        }
        fast++
    }
    return slow
}

注意这里和有序数组去重的解法有一个细节差异，我们这里是先给 nums[slow] 赋值然后再给 slow++，这样可以保证 nums[0..slow-1] 是不包含值为 val 的元素的，最后的结果数组长度就是 slow。

滑动窗口

滑动窗口算法技巧主要用来解决子数组问题，比如让你寻找符合某个条件的最长/最短子数组。

模板

框架中两处 ... 表示的更新窗口数据的地方，在具体的题目中，你需要做的就是往这里面填代码逻辑。而且，这两个 ... 处的操作分别是扩大和缩小窗口的更新操作，等会你会发现它们操作是完全对称的。

// 滑动窗口算法伪码框架
func slidingWindow(s string) {
    // 用合适的数据结构记录窗口中的数据，根据具体场景变通
    // 比如说，我想记录窗口中元素出现的次数，就用 map
    // 如果我想记录窗口中的元素和，就可以只用一个 int
    var window = ...

    left, right := 0, 0
    for right < len(s) {
        // c 是将移入窗口的字符
        c := s[right]
        window[c]++
        // 增大窗口
        right++
        // 进行窗口内数据的一系列更新
        ...

        // *** debug 输出的位置 ***
        // 注意在最终的解法代码中不要 print
        // 因为 IO 操作很耗时，可能导致超时
        fmt.Println("window: [",left,", ",right,")")
        // ***********************

        // 判断左侧窗口是否要收缩
        for left < right && window needs shrink { //replace "window needs shrink" with actual condition
            // d 是将移出窗口的字符
            d := s[left]
            window[d]--
            // 缩小窗口
            left++
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

例题

LeetCode	难度
438.找到字符串中所有字母异位词	🟡
567.字符串的排列	🟡
3.无重复字符的最长子串	🟡
76.最小覆盖子串	🔴

76.最小覆盖子串

给你一个字符串 s、一个字符串 t。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 ""。

注意：

对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"
解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。

func minWindow(s string, t string) string {
    // need 记录目标字符串中每个字符出现的次数
    // window 记录滑动窗口中相应字符出现的次数
    need, window := make(map[byte]int), make(map[byte]int)
    for i := range t {
        need[t[i]]++
    }

    left, right := 0, 0
    valid := 0
    // 记录最小覆盖子串的起始索引及长度
    start, length := 0, math.MaxInt32
    for right < len(s) {
        // c 是将移入窗口的字符
        c := s[right]
        // 扩大窗口
        right++
        // 进行窗口内数据的一系列更新
        if _, ok := need[c]; ok {
            window[c]++
            if window[c] == need[c] {
                valid++
            }
        }

        // 判断左侧窗口是否要收缩
        for valid == len(need) {
            // 在这里更新最小覆盖子串
            if right - left < length {
                start = left
                length = right - left
            }
            // d 是将移出窗口的字符
            d := s[left]
            // 缩小窗口
            left++
            // 进行窗口内数据的一系列更新
            if _, ok := need[d]; ok {
                if window[d] == need[d] {
                    valid--
                }
                window[d]--
            }
        }
    }
    // 返回最小覆盖子串
    if length == math.MaxInt32 {
        return ""
    }
    return s[start : start+length]
}

567.字符串的排列

给你两个字符串 s1 和 s2 ，写一个函数来判断 s2 是否包含 s1 的排列。如果是，返回 true；否则，返回 false。

换句话说，s1 的排列之一是 s2 的子串。

示例 1：

输入：s1 = "ab" s2 = "eidbaooo"
输出：true
解释：s2 包含 s1 的排列之一 ("ba").

示例 2：

输入：s1= "ab" s2 = "eidboaoo"
输出：false

提示：

1 <= s1.length, s2.length <= 104
s1 和 s2 仅包含小写字母

这种题目，是明显的滑动窗口算法，相当给你一个 s 和一个 t，请问你 s 中是否存在一个子串，包含 t 中所有字符且不包含其他字符。

// 判断 s 中是否存在 t 的排列
func checkInclusion(t string, s string) bool {
	need := make(map[byte]int)
	window := make(map[byte]int)

	for c := range t {
		need[t[c]]++
	}

	left, right := 0, 0
	valid := 0
	for right < len(s) {
		c := s[right]
		right++
        // 进行窗口内数据的一系列更新
		if _, ok := need[c]; ok {
			window[c]++
			if window[c] == need[c] {
				valid++
			}
		}

        // 判断左侧窗口是否要收缩
        // 窗口长度等于 t 时，左侧指针 left 会收缩窗口，保证窗口中没有多余字符
		for right-left == len(t) {
            // 在这里判断是否找到了合法的子串
			if valid == len(need) {
				return true
			}
			d := s[left]
			left++
            // 进行窗口内数据的一系列更新
			if _, ok := need[d]; ok {
				if window[d] == need[d] {
					valid--
				}
				window[d]--
			}
		}
	}
    // 未找到符合条件的子串
	return false
}

438.找到字符串中所有字母异位词

给定两个字符串 s 和 p，找到 s 中所有 p 的异位词的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

示例 1:

输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。

这个所谓的字母异位词，不就是排列吗，搞个高端的说法就能糊弄人了吗？相当于，输入一个串 s，一个串 p，找到 s 中所有 p 的排列，返回它们的起始索引。

func findAnagrams(s string, p string) []int {
    // 记录结果
	ans := []int{}
	need := make(map[byte]int)
	window := make(map[byte]int)

	for i := range p {
		need[p[i]]++
	}

	left, right := 0, 0
	valid := 0

	for right < len(s) {
		c := s[right]
		right++
        // 进行窗口内数据的一系列更新
		if _, ok := need[c]; ok {
			window[c]++
			if window[c] == need[c] {
				valid++
			}
		}

        // 判断左侧窗口是否要收缩
        // 保证窗口长度始终和 p 的长度一致
		for right-left == len(p) {
            // 当窗口符合条件时，把起始索引加入 res
			if valid == len(need) {
				ans = append(ans, left)
			}

			d := s[left]
			left++
            // 进行窗口内数据的一系列更新
			if _, ok := need[d]; ok {
				if window[d] == need[d] {
					valid--
				}
				window[d]--
			}
		}
	}
	return ans
}

4.最长无重复子串

给定一个字符串 s，请你找出其中不含有重复字符的最长子串的长度。

示例 1:

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

这个题终于有了点新意，不是一套框架就出答案，不过反而更简单了，稍微改一改框架就行了：

这就是变简单了，连 need 和 valid 都不需要，而且更新窗口内数据也只需要简单的更新计数器 window 即可。
当 window[c] 值大于 1 时，说明窗口中存在重复字符，不符合条件，就该移动 left 缩小窗口了嘛。

func lengthOfLongestSubstring(s string) int {
	window := make(map[byte]int)
	left, right := 0, 0
	// 记录结果
	res := 0

	for right < len(s) {
		c := s[right]
		right++
		// 进行窗口内数据的一系列更新
		window[c] = window[c] + 1

		// 判断左侧窗口是否要收缩
		for window[c] > 1 {
			d := s[left]
			left++

			// 进行窗口内数据的一系列更新
			window[d] = window[d] - 1
		}

		// 在这里更新答案
		if res < right-left {
			res = right - left
		}
	}
	return res
}

左右指针

二分查找

1.分析二分查找代码时，不要出现 else，全部展开成 else if 方便理解。把逻辑写对之后再合并分支，提升运行效率。
2.注意「搜索区间」和 while 的终止条件，如果存在漏掉的元素，记得在最后检查。
3.如果将「搜索区间」全都统一成两端都闭，好记，只要稍改 nums[mid] == target 条件处的代码和返回的逻辑即可，推荐拿小本本记下，作为二分搜索模板。

// 基本二分查找
func binarySearch(nums []int, target int) int {
    left, right := 0, len(nums)-1
    for left <= right {
        mid := left + (right - left) / 2
        if nums[mid] < target {
            left = mid + 1
        } else if nums[mid] > target {
            right = mid - 1
        } else if nums[mid] == target {
            // 直接返回
            return mid
        }
    }
    // 直接返回
    return -1
}

// 寻找左边界的二分查找
func leftBound(nums []int, target int) int {
    left, right := 0, len(nums)-1
    for left <= right {
        mid := left + (right - left) / 2
        if nums[mid] < target {
            left = mid + 1
        } else if nums[mid] > target {
            right = mid - 1
        } else if nums[mid] == target {
            // 别返回，锁定左侧边界
            right = mid - 1
        }
    }
    // 判断 target 是否存在于 nums 中
    if left < 0 || left >= len(nums) {
        return -1
    }
    // 判断一下 nums[left] 是不是 target
    if nums[left] == target {
        return left
    }
    return -1
}

// 寻找右边界的二分查找
func rightBound(nums []int, target int) int {
    left, right := 0, len(nums)-1
    for left <= right {
        mid := left + (right - left) / 2
        if nums[mid] < target {
            left = mid + 1
        } else if nums[mid] > target {
            right = mid - 1
        } else if nums[mid] == target {
            // 别返回，锁定右侧边界
            left = mid + 1
        }
    }
    
    if right < 0 || right >= len(nums) {
        return -1
    }
    if nums[right] == target {
        return right
    }
    return -1
}

n 数之和

总结来说，这类 nSum 问题就是给你输入一个数组 nums 和一个目标和 target，让你从 nums 选择 n 个数，使得这些数字之和为 target。

LeetCode	难度
1.两数之和	🟢
15.三数之和	🟠
18.四数之和	🟠

1.两数之和

假设输入一个数组 nums 和一个目标和 target，请你返回 nums 中所有能够凑出 target 的两个元素的值，其中不能出现重复，比如说输入为 nums = [1,3,1,2,2,3], target = 4，那么算法返回的结果就是：[[1,3],[2,2]]（注意，我要求返回元素，而不是索引）。比如 [1,3] 和 [3,1] 就算重复，只能算一次。

我们可以先对 nums 排序，然后利用左右双指针技巧，从两端相向而行。当给 res 加入一次结果后，lo 和 hi 不仅应该相向而行，而且应该跳过所有重复的元素。

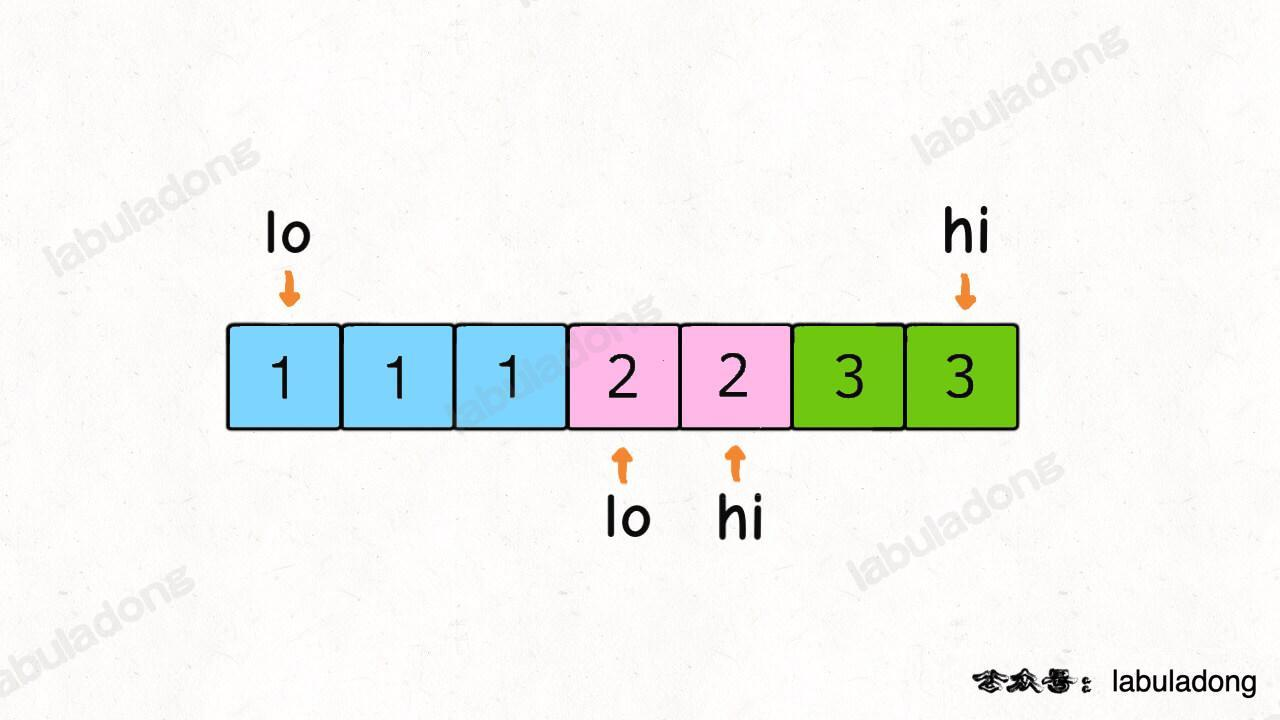
func twoSum(nums []int, target int) [][]int {
    // nums 数组必须有序
    sort.Ints(nums)
    var lo, hi int = 0, len(nums) - 1
    var res [][]int
    for lo < hi {
        sum := nums[lo] + nums[hi]
        // 记录索引 lo 和 hi 最初对应的值
        left, right := nums[lo], nums[hi]
        if sum < target {
            lo++
        } else if sum > target {
            hi--
        } else {
            res = append(res, []int{left, right})
            
            // 跳过所有重复的元素
            for lo < hi && nums[lo] == left {
                lo++
            }
            for lo < hi && nums[hi] == right {
                hi--
            }
        }
    }
    return res
}

注意 LeetCode 的 1.两数之和一题中，要求返回的是数组下标，因此不能对原数组进行排序，需要使用哈希表的做法，解法参考：hot100#两数之和。

15.三数之和

给你一个整数数组 nums，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k，同时还满足 nums[i] + nums[j] + nums[k] == 0。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

穷举第一个数，并保证一个数不重复，然后复用 twoSum 函数会保证后面两个数不重复。将 twoSum 返回的结果加上第一个数放到结果列表中。

// 计算数组 nums 中所有和为 target 的三元组
func threeSum(nums []int) [][]int {
    // 数组得排个序 
	sort.Ints(nums)
	var res [][]int
	n := len(nums)
    // 穷举 threeSum 的第一个数
	for i := 0; i < n; i++ {
        // 跳过第一个数字重复的情况，否则会出现重复结果
        if i > 0 && nums[i] == nums[i-1] {
            continue
        }

        // 对 target - nums[i] 计算 twoSum
		tuples := twoSum(nums, i+1, 0-nums[i])
        // 如果存在满足条件的二元组，再加上 nums[i] 就是结果三元组
		for _, tuple := range tuples {
			tuple = append(tuple, nums[i])
			res = append(res, tuple)
		}
	}
	return res
}

// 从 nums[start] 开始，计算有序数组 nums 中所有和为 target 的二元组
func twoSum(nums []int, start int, target int) [][]int {
	var res [][]int
    // 左指针改为从 start 开始，其他不变
	lo, hi := start, len(nums)-1
	for lo < hi {
		sum := nums[lo] + nums[hi]
		left, right := nums[lo], nums[hi]
		if sum < target {
			lo++
		} else if sum > target {
			hi--
		} else {
			res = append(res, []int{nums[lo], nums[hi]})

			for lo < hi && nums[lo] == left {
				lo++
			}
			for lo < hi && nums[hi] == right {
				hi--
			}
		}
	}
	return res
}

18.四数之和

给你一个由 n 个整数组成的数组 nums，和一个目标值 target。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]]（若两个四元组元素一一对应，则认为两个四元组重复）：

0 <= a, b, c, d < n
a、b、c 和 d 互不相同
nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按任意顺序返回答案。

示例 1：

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

fourSum 完全就可以用相同的思路：穷举第一个数字，然后调用 threeSum 函数计算剩下三个数，最后组合出和为 target 的四元组。

我们可以使用一个统一的 nSum 递归函数来解决，这样如果有 100Sum 的问题也一样可以处理。

func fourSum(nums []int, target int) [][]int {
    sort.Ints(nums)
    return nSum(nums, 4, 0, target)
}

// 注意：调用这个函数之前一定要先给 nums 排序
// n 填写想求的是几数之和，start 从哪个索引开始计算（一般填 0），target 填想凑出的目标和
func nSum(nums []int, n int, start int, target int) [][]int {
    sz := len(nums)
    res := [][]int{}
    // 至少是 2Sum，且数组大小不应该小于 n
    if n < 2 || sz < n {
        return res
    }
    // 2Sum 是 base case
    if n == 2 {
        lo, hi := start, sz-1
        for lo < hi {
            sum := nums[lo] + nums[hi]
            left, right := nums[lo], nums[hi]
            if sum < target {
                for lo < hi && nums[lo] == left {
                    lo++
                }
            } else if sum > target {
                for lo < hi && nums[hi] == right {
                    hi--
                }
            } else {
                res = append(res, []int{left, right})
                for lo < hi && nums[lo] == left {
                    lo++
                }
                for lo < hi && nums[hi] == right {
                    hi--
                }
            }
        }
    } else {
        // n > 2 时，递归计算 (n-1)Sum 的结果
        for i := start; i < sz; i++ {
            // 跳过重复值
            if i > start && nums[i] == nums[i-1] {
                continue
            }
            subs := nSum(nums, n-1, i+1, target-nums[i])
            for _, sub := range subs {
                // (n-1)Sum 加上 nums[i] 就是 nSum
                res = append(res, append(sub, nums[i]))
            }
        }
    }
    return res
}

反转数组

344.反转字符串

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。

不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

示例 1：

输入：s = ["h","e","l","l","o"]
输出：["o","l","l","e","h"]

func reverseString(s []byte)  {
    // 一左一右两个指针相向而行
    left, right := 0, len(s)-1
    for left < right {
        // 交换 s[left] 和 s[right]
        s[left], s[right] = s[right], s[left]
        left++
        right--
    }
}

回文串判断

回文串就是正着读和反着读都一样的字符串。比如说字符串 aba 和 abba 都是回文串，因为它们对称，反过来还是和本身一样；反之，字符串 abac 就不是回文串。

现在你应该能感觉到回文串问题和左右指针肯定有密切的联系，比如让你判断一个字符串是不是回文串，你可以写出下面这段代码：

func isPalindrome(s string) bool {
    // 一左一右两个指针相向而行
    left, right := 0, len(s) - 1
    for left < right {
        if s[left] != s[right] {
            return false
        }
        left++
        right--
    }
    return true
}

5.最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

遍历 s，分别找到以 i 为中心的奇数和偶数的最长回文子串，最后返回最长的回文子串。

func longestPalindrome(s string) string {
    var res string
    for i := 0; i < len(s); i++ {
        // 以 s[i] 为中心的最长回文子串
        s1 := palindrome(s, i, i)
        // 以 s[i] 和 s[i+1] 为中心的最长回文子串
        s2 := palindrome(s, i, i+1)
        // res = longest(res, s1, s2)
        if len(res) < len(s1) {
            res = s1
        }
        if len(res) < len(s2) {
            res = s2
        }
    }
    return res
}
// 在 s 中寻找以 s[l] 和 s[r] 为中心的最长回文串
func palindrome(s string, l int, r int) string {
    // 防止索引越界
    for l >= 0 && r < len(s) && s[l] == s[r] {
        // 双指针，向两边展开
        l--
        r++
    }
    // 返回以 s[l] 和 s[r] 为中心的最长回文串
    return s[l+1 : r]
}

二维数组遍历

顺/逆时针旋转矩阵

我们可以先将 n x n 矩阵 matrix 按照左上到右下的对角线进行镜像对称：

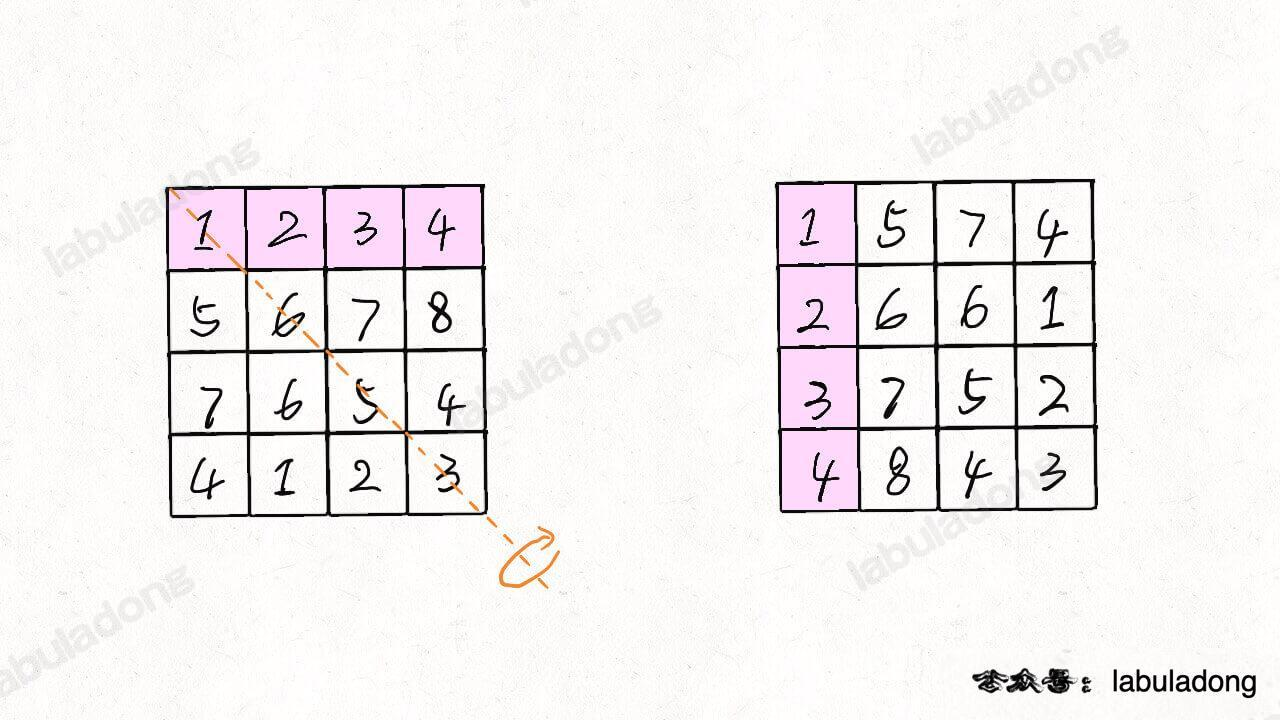
然后再对矩阵的每一行进行反转：

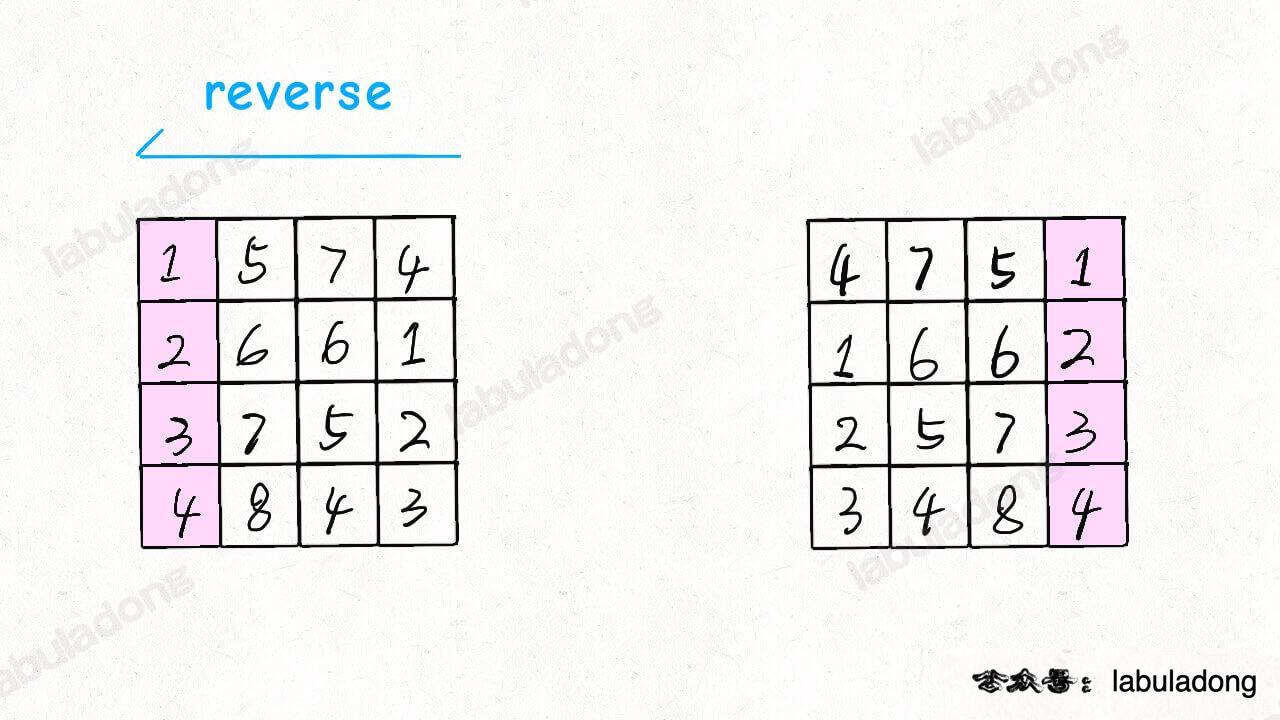
发现结果就是 matrix 顺时针旋转 90 度的结果：

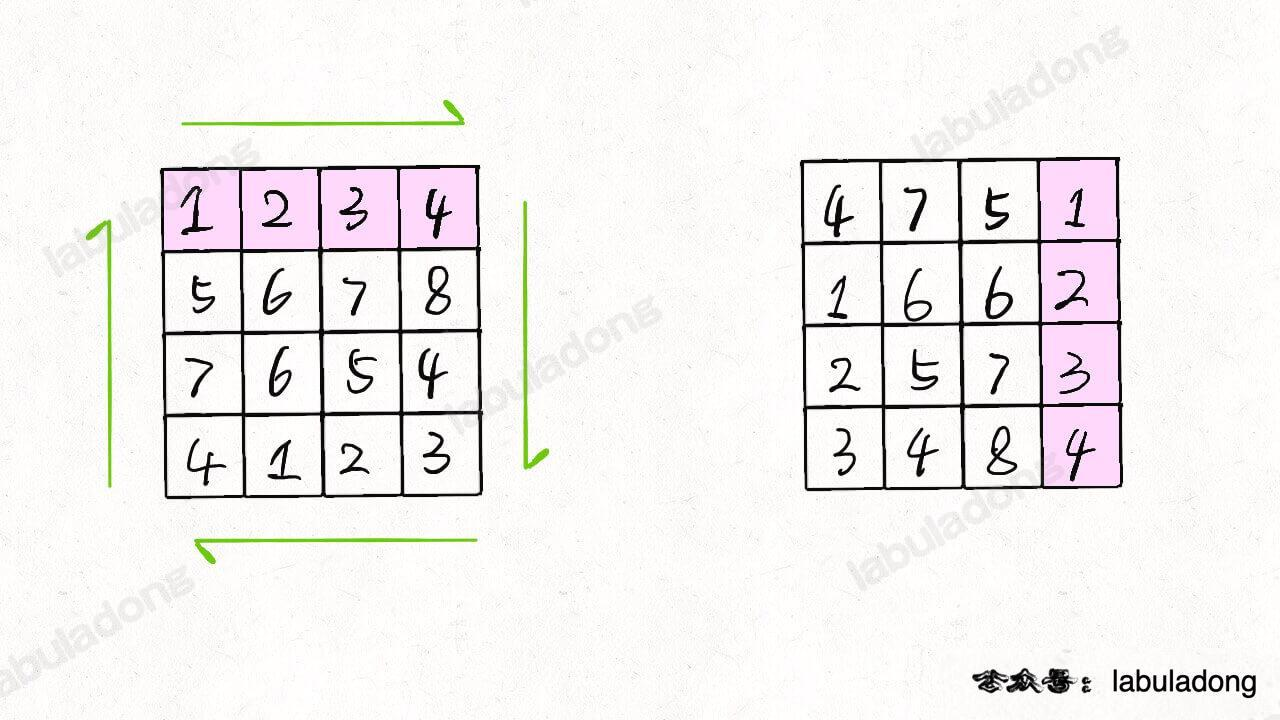
var rotate = func(matrix [][]int) {
    // 将二维矩阵原地顺时针旋转 90 度
    n := len(matrix)
    // 先沿对角线镜像对称二维矩阵
    for i := 0; i < n; i++ {
        for j := i; j < n; j++ {
            // swap(matrix[i][j], matrix[j][i]);
            matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
        }
    }
    // 然后反转二维矩阵的每一行
    for _, row := range matrix {
        reverse(row)
    }
}

// 翻转一维数组
func reverse(arr []int) {
    i, j := 0, len(arr) - 1
    for j > i {
        // swap(arr[i], arr[j]);
        arr[i], arr[j] = arr[j], arr[i]
        i++
        j--
    }
}

如何将矩阵逆时针旋转 90 度呢？思路是类似的，只要通过另一条对角线镜像对称矩阵，然后再反转每一行，就得到了逆时针旋转矩阵的结果：

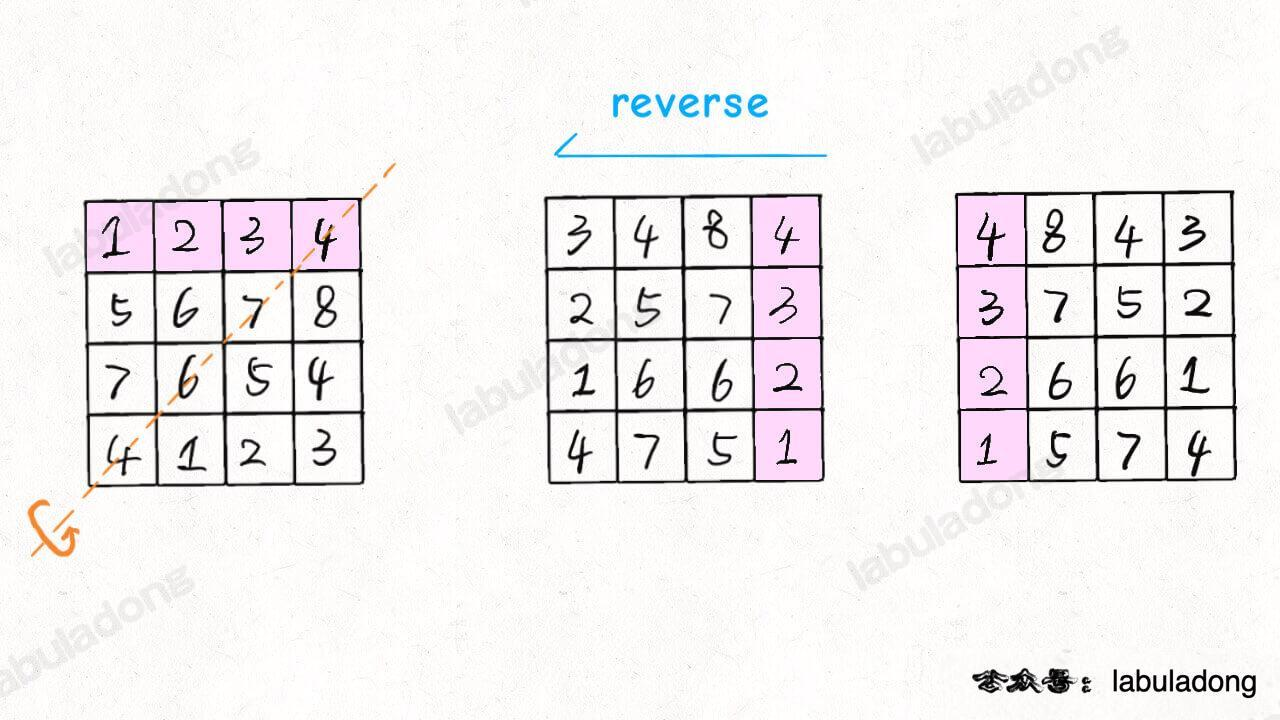
// 将二维矩阵原地逆时针旋转 90 度
func rotate2(matrix [][]int) {
    n := len(matrix)
    // 沿左下到右上的对角线镜像对称二维矩阵
    for i := 0; i < n; i++ {
        for j := 0; j < n - i; j++ {
            // swap(matrix[i][j], matrix[n-j-1][n-i-1])
            temp := matrix[i][j]
            matrix[i][j] = matrix[n - j - 1][n - i - 1]
            matrix[n - j - 1][n - i - 1] = temp
        }
    }

    // 然后反转二维矩阵的每一行
    for _, row := range matrix {
        reverse(row)
    }
}

func reverse(arr []int) {
    // 见上文
}

矩阵的螺旋遍历

54.螺旋矩阵

解题的核心思路是按照右、下、左、上的顺序遍历数组，并使用四个变量圈定未遍历元素的边界：

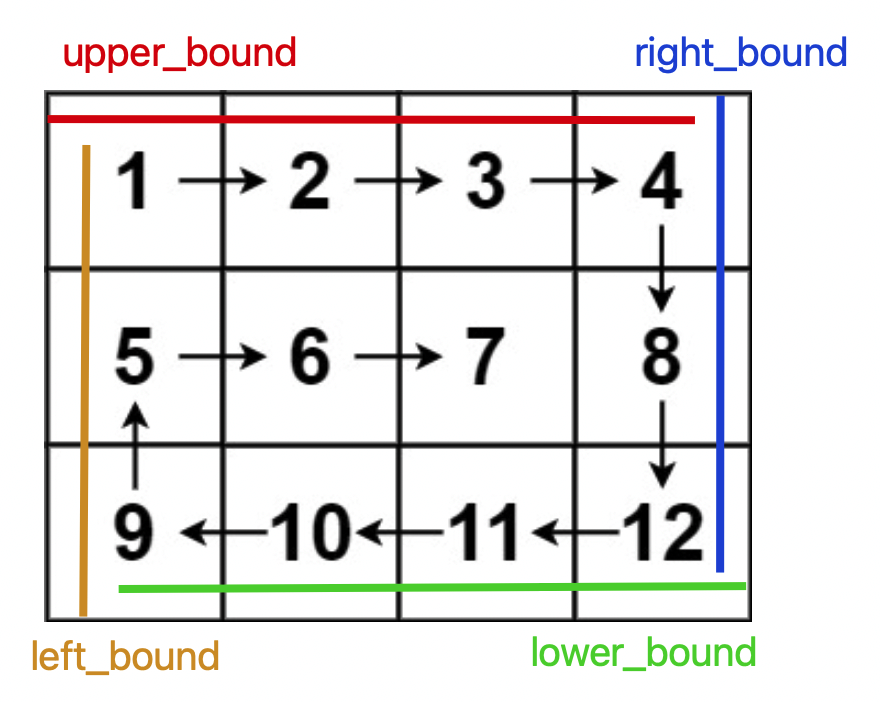
func spiralOrder(matrix [][]int) []int {
    var res []int
    m := len(matrix)
    n := len(matrix[0])
    upper_bound := 0
    lower_bound := m - 1
    left_bound := 0
    right_bound := n - 1
    // res.size() == m * n 则遍历完整个数组
    for len(res) < m*n {
        if upper_bound <= lower_bound {
            // 在顶部从左向右遍历
            for j := left_bound; j <= right_bound; j++ {
                res = append(res, matrix[upper_bound][j])
            }
            // 上边界下移
            upper_bound++
        }
        
        if left_bound <= right_bound {
            // 在右侧从上向下遍历
            for i := upper_bound; i <= lower_bound; i++ {
                res = append(res, matrix[i][right_bound])
            }
            // 右边界左移
            right_bound--
        }
        
        if upper_bound <= lower_bound {
            // 在底部从右向左遍历
            for j := right_bound; j >= left_bound; j-- {
                res = append(res, matrix[lower_bound][j])
            }
            // 下边界上移
            lower_bound--
        }
        
        if left_bound <= right_bound {
            // 在左侧从下向上遍历
            for i := lower_bound; i >= upper_bound; i-- {
                res = append(res, matrix[i][left_bound])
            }
            // 左边界右移
            left_bound++
        }
    }
    return res
}

59.螺旋矩阵 II

与 54.螺旋矩阵一题类似，只不过是反过来，让你按照螺旋的顺序生成矩阵：

func generateMatrix(n int) [][]int {
    matrix := make([][]int, n)
    for i := range matrix {
        matrix[i] = make([]int, n)
    }
    upper_bound, lower_bound := 0, n - 1
    left_bound, right_bound := 0, n - 1
    // 需要填入矩阵的数字
    num := 1

    for num <= n * n {
        if upper_bound <= lower_bound {
            // 在顶部从左向右遍历
            for j := left_bound; j <= right_bound; j++ {
                matrix[upper_bound][j] = num
                num++
            }
            // 上边界下移
            upper_bound++
        }

        if left_bound <= right_bound {
            // 在右侧从上向下遍历
            for i := upper_bound; i <= lower_bound; i++ {
                matrix[i][right_bound] = num
                num++
            }
            // 右边界左移
            right_bound--
        }

        if upper_bound <= lower_bound {
            // 在底部从右向左遍历
            for j := right_bound; j >= left_bound; j-- {
                matrix[lower_bound][j] = num
                num++
            }
            // 下边界上移
            lower_bound--
        }

        if left_bound <= right_bound {
            // 在左侧从下向上遍历
            for i := lower_bound; i >= upper_bound; i-- {
                matrix[i][left_bound] = num
                num++
            }
            // 左边界右移
            left_bound++
        }
    }
    return matrix
}

前缀和

区域和检索 - 数组不可变

给定一个整数数组 nums，处理以下类型的多个查询：

计算索引 left 和 right （包含 left 和 right）之间的 nums 元素的和，其中 left <= right，实现 NumArray 类：

NumArray(int[] nums) 使用数组 nums 初始化对象
int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的总和，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + ... + nums[right])

示例 1：

输入：
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出：
[null, 1, -1, -3]

解释：
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1)) 
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))

sumRange 函数需要计算并返回一个索引区间之内的元素和，没学过前缀和的人可能写出如下代码：

type NumArray struct {
    nums []int
}

func Constructor(nums []int) NumArray {
    return NumArray {
        nums: nums,
    }
}

func (this *NumArray) SumRange(left int, right int) int {
    sum := 0
    for i := left; i <= right; i++ {
        sum += this.nums[i]
    }
    return sum
}

这个解法每次调用 sumRange 函数时，都要进行一次 for 循环遍历，时间复杂度为 O(N)，而 sumRange 的调用频率可能非常高，所以这个算法的效率很低。

正确的解法是使用前缀和技巧进行优化，使得 sumRange 函数的时间复杂度为 O(1)：

type NumArray struct {
    // 前缀和数组
    PreSum []int
}

// 输入一个数组，构造前缀和
func Constructor(nums []int) NumArray {
    // PreSum[0] = 0，便于计算累加和
    preSum := make([]int, len(nums)+1)
    // 计算 nums 的累加和
    for i := 1; i < len(preSum); i++ {
        preSum[i] = preSum[i-1] + nums[i-1]
    }
    return NumArray{PreSum: preSum}
}

// 查询闭区间 [left, right] 的累加和
func (this *NumArray) SumRange(left int, right int) int {   
    return this.PreSum[right+1] - this.PreSum[left]
}

看这个 preSum 数组，如果我想求索引区间 [0, 2] 内的所有元素之和，就可以通过 preSum[3] - preSum[0] 得出（结果是 1）。如果想求 [2, 5] 内的元素和，则用 preSum[6] - preSum[2] 得出（结果是 3）。因为为了便于计算累加和，将 preSum[0] 设置为 0，所以在计算累加和时 preSum 的下标要加 1。

304. 二维区域和检索 - 矩阵不可变

给定一个二维矩阵 matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1)，右下角为 (row2, col2)。

实现 NumMatrix 类：

NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回左上角 (row1, col1)、右下角 (row2, col2) 所描述的子矩阵的元素总和。

示例 1：

输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

任意子矩阵的元素和可以转化成它周边几个大矩阵的元素和的运算：

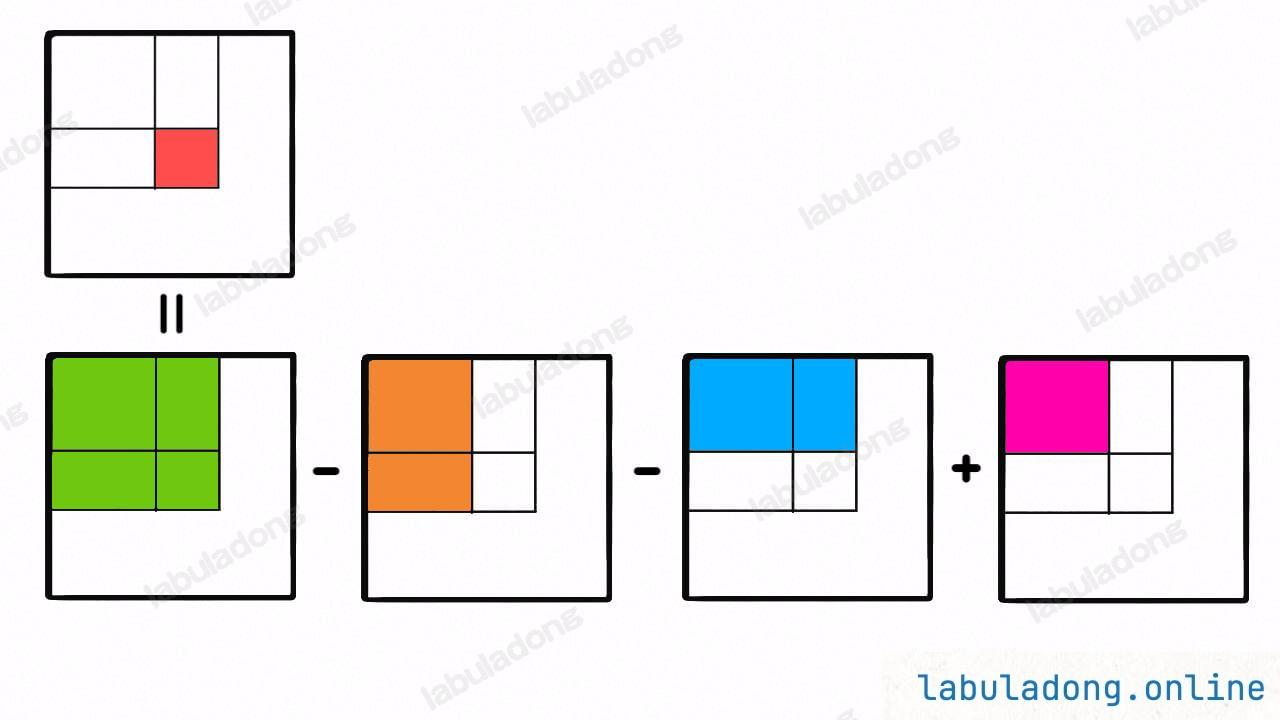
而这四个大矩阵有一个共同的特点，就是左上角都是 (0, 0) 原点。

那么做这道题更好的思路和一维数组中的前缀和是非常类似的，我们可以维护一个二维 preSum 数组，专门记录以原点为顶点的矩阵的元素之和，就可以用几次加减运算算出任何一个子矩阵的元素和：

type NumMatrix struct {
    // preSum[i][j] 记录矩阵 [0, 0, i-1, j-1] 的元素和
    preSum [][]int
}

func Constructor(matrix [][]int) NumMatrix {
    // 初始化二维数组
    preSum := make([][]int, len(matrix) + 1)
    for i := 0; i < len(preSum); i++ {
        preSum[i] = make([]int, len(matrix[0]) + 1)
    }

    // 构建前缀和数组
    // preSum[i][j] 记录矩阵 [0, 0, i-1, j-1] 的元素和
    for i := 1; i < len(preSum); i ++ {
        for j := 1; j < len(preSum[0]); j++ {
            preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i-1][j-1] - preSum[i-1][j-1];
        }
    }
    return NumMatrix{preSum}
}

func (this *NumMatrix) SumRegion(row1 int, col1 int, row2 int, col2 int) int {
    return this.preSum[row2+1][col2+1] - this.preSum[row1][col2+1] - this.preSum[row2+1][col1] + this.preSum[row1][col1] 
}

和为 K 的子数组

给你一个整数数组 nums 和一个整数 k，请你统计并返回该数组中和为 k 的子数组的个数。

子数组是数组中元素的连续非空序列。

示例 1：

输入：nums = [1,1,1], k = 2
输出：2

示例 2：

输入：nums = [1,2,3], k = 3
输出：2

用 prefixSum 表示当前的前缀和。
维护一个哈希表 countMap，其中键为前缀和，值为该前缀和出现的次数。
遍历数组时，通过 prefixSum - k 判断是否存在之前的前缀和满足条件。

func subarraySum(nums []int, k int) int {
    countMap := make(map[int]int)
    countMap[0] = 1 // 初始前缀和为 0 的情况
    prefixSum := 0
    count := 0

    for _, num := range nums {
        prefixSum += num
        // 检查是否存在前缀和使得当前子数组和为 k
        if val, exists := countMap[prefixSum-k]; exists {
            count += val
        }
        // 更新当前前缀和的出现次数
        countMap[prefixSum]++
    }

    return count
}

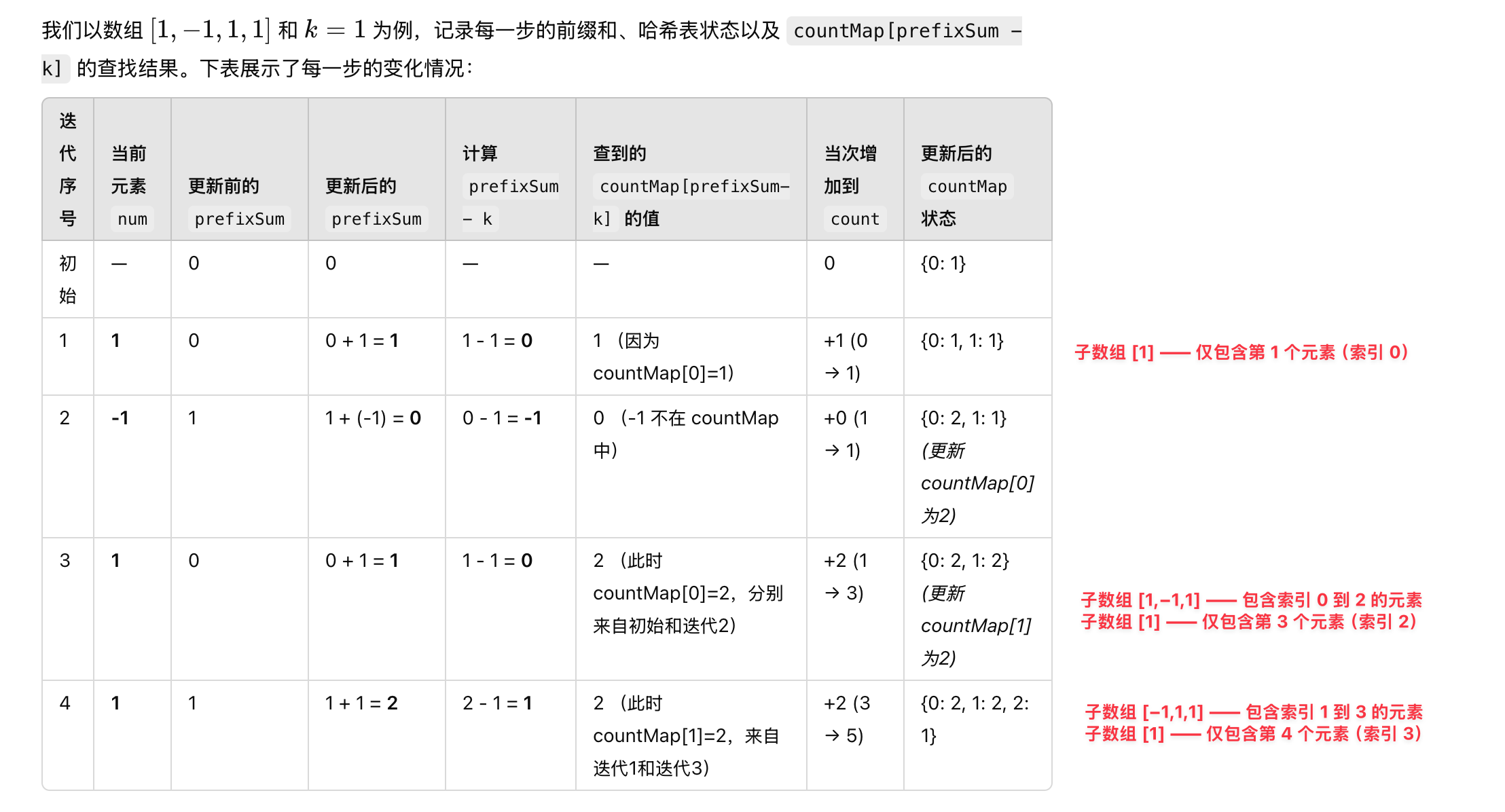
核心思想：对于当前的前缀和 prefixSum，如果存在之前的某个前缀和为 prefixSum - k，那么从该位置到当前位置的子数组和即为 k。该前缀和出现的次数决定了能组成多少个满足条件的子数组。

差分数组

差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。

比如说，我给你输入一个数组 nums，然后又要求给区间 nums[2..6] 全部加 1，再给 nums[3..9] 全部减 3，再给 nums[0..4] 全部加 2...

370.区间加法

假设你有一个长度为 n 的数组，初始情况下所有的数字均为 0，你将会被给出 k 个更新的操作。

其中，每个操作会被表示为一个三元组：[startIndex, endIndex, inc]，你需要将子数组 A[startIndex ... endIndex]（包括 startIndex 和 endIndex）增加 inc。

请你返回 k 次操作后的数组。

示例：

输入: length = 5, updates = [[1,3,2],[2,4,3],[0,2,-2]]
输出: [-2,0,3,5,3]

解释:
初始状态:
[0,0,0,0,0]

进行了操作 [1,3,2] 后的状态:
[0,2,2,2,0]

进行了操作 [2,4,3] 后的状态:
[0,2,5,5,3]

进行了操作 [0,2,-2] 后的状态:
[-2,0,3,5,3]

解法如下：

func getModifiedArray(length int, updates [][]int) []int {
    // nums 初始化为全 0
    nums := make([]int, length)
    // 构造差分解法
    df := NewDifference(nums)
    for _, update := range updates {
        i, j, val := update[0], update[1], update[2]
        df.Increment(i, j, val)
    }
    return df.Result()
}

// 差分数组
type Difference struct {
    diff []int
}

func NewDifference(nums []int) *Difference {
    assert(len(nums) > 0)
    diff := make([]int, len(nums))
    // 构造差分数组
    diff[0] = nums[0]
    for i := 1; i < len(nums); i++ {
        diff[i] = nums[i] - nums[i-1]
    }
    return &Difference{diff: diff}
}

// 给闭区间 [i, j] 增加 val（可以是负数）
func (d *Difference) Increment(i, j, val int) {
    d.diff[i] += val
    if j+1 < len(d.diff) {
        d.diff[j+1] -= val
    }
}

// 根据差分数组构造结果数组
func (d *Difference) Result() []int {
    res := make([]int, len(d.diff))
    // 根据差分数组构造结果数组
    res[0] = d.diff[0]
    for i := 1; i < len(d.diff); i++ {
        res[i] = res[i-1] + d.diff[i]
    }
    return res
}

func assert(condition bool) {
    if !condition {
        panic("condition failed")
    }
}

栈

71.简化路径

给你一个字符串 path，表示指向某一文件或目录的 Unix 风格绝对路径（以 '/' 开头），请你将其转化为更加简洁的规范路径。

在 Unix 风格的文件系统中规则如下：

一个点 '.' 表示当前目录本身。
此外，两个点 '..' 表示将目录切换到上一级（指向父目录）。
任意多个连续的斜杠（即，'//' 或 '///'）都被视为单个斜杠 '/'。
任何其他格式的点（例如，'...' 或 '....'）均被视为有效的文件/目录名称。

返回的简化路径必须遵循下述格式：

始终以斜杠 '/' 开头。
两个目录名之间必须只有一个斜杠 '/'。
最后一个目录名（如果存在）不能以 '/' 结尾。
此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含 '.' 或 '..'）。

返回简化后得到的规范路径。

示例 1：

输入：path = "/home/"
输出："/home"
解释：
应删除尾随斜杠。

示例 2：

输入：path = "/home//foo/"
输出："/home/foo"
解释：
多个连续的斜杠被单个斜杠替换。

示例 3：

输入：path = "/home/user/Documents/../Pictures"
输出："/home/user/Pictures"
解释：
两个点 ".." 表示上一级目录（父目录）。

这题比较简单，利用栈先进后出的特性处理上级目录 ..，最后组装化简后的路径即可。

func simplifyPath(path string) string {
    parts := strings.Split(path, "/")
    stk := []string{}
    // 借助栈计算最终的文件夹路径
    for _, part := range parts {
        if part == "" || part == "." {
            continue
        }
        if part == ".." {
            if len(stk) > 0 {
                stk = stk[:len(stk)-1]
            }
            continue
        }
        stk = append(stk, part)
    }
    // 栈中存储的文件夹组成路径
    res := ""
    for _, dir := range stk {
        res += "/" + dir
    }
    if res == "" {
        return "/"
    }
    return res
}

单调栈

下一个更大元素 I

nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置右侧的第一个比 x 大的元素。

给你两个没有重复元素的数组 nums1 和 nums2，下标从 0 开始计数，其中nums1 是 nums2 的子集。

对于每个 0 <= i < nums1.length，找出满足 nums1[i] == nums2[j] 的下标 j，并且在 nums2 确定 nums2[j] 的下一个更大元素。如果不存在下一个更大元素，那么本次查询的答案是 -1。

返回一个长度为 nums1.length 的数组 ans 作为答案，满足 ans[i] 是如上所述的下一个更大元素。

示例 1：

输入：nums1 = [4,1,2], nums2 = [1,3,4,2].
输出：[-1,3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：
- 4 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。
- 1 ，用加粗斜体标识，nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ，用加粗斜体标识，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。

因为题目说 nums1 是 nums2 的子集，那么我们先把 nums2 中每个元素的下一个更大元素算出来存到一个映射里，然后再让 nums1 中的元素去查表即可。

func nextGreaterElement(nums1 []int, nums2 []int) []int {
    // 记录 nums2 中每个元素的下一个更大元素
    greater := calculateGreaterElement(nums2)
    // 转化成映射：元素 x -> x 的下一个最大元素
    greaterMap := make(map[int]int)
    for i := 0; i < len(nums2); i++ {
        greaterMap[nums2[i]] = greater[i]
    }
    // nums1 是 nums2 的子集，所以根据 greaterMap 可以得到结果
    res := make([]int, len(nums1))
    for i := 0; i < len(nums1); i++ {
        res[i] = greaterMap[nums1[i]]
    }
    return res
}

func calculateGreaterElement(nums []int) []int {
    n := len(nums)
    res := make([]int, n) // 结果数组
    s := make([]int, 0)   // 单调递减栈

    // 倒序遍历 nums
    for i := n - 1; i >= 0; i-- {
        // 弹出栈内小于等于 nums[i] 的元素
        for len(s) != 0 && s[len(s)-1] <= nums[i] {
            s = s[:len(s)-1] // 移除栈顶
        }
        // 记录右侧第一个更大的元素
        if len(s) == 0 {
            res[i] = -1
        } else {
            res[i] = s[len(s)-1]
        }
        // 当前元素入栈
        s = append(s, nums[i])
    }
    return res
}

每日温度

给定一个整数数组 temperatures，表示每天的温度，返回一个数组 answer，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

示例 1:

输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

核心思路：

使用单调递减栈维护「尚未找到更高温度的索引 i」。
从右向左遍历 temperatures，保证栈内存储的索引 s[len(s)-1] 对应的温度始终大于当前温度。
如果栈顶温度比当前温度高，则栈顶索引 s[len(s)-1] 就是 i 之后的第一个更高温度的索引，计算 res[i]。
如果当前温度更高，弹出栈顶元素，继续查找更大的温度。

func dailyTemperatures(temperatures []int) []int {
    n := len(temperatures)
    res := make([]int, n) // 结果数组，默认值为 0
    s := make([]int, 0)   // 单调递减栈，存储索引（不是温度）

    // 从右向左遍历温度数组
    for i := n - 1; i >= 0; i-- {
        // 维护单调递减栈
        // 弹出栈中所有比当前温度小或相等的索引
        for len(s) > 0 && temperatures[s[len(s)-1]] <= temperatures[i] {
            s = s[:len(s)-1] // 出栈
        }
        
        // 计算索引间距
        if len(s) == 0 {
            res[i] = 0 // 栈为空，说明 i 之后没有更高温度
        } else {
            res[i] = s[len(s)-1] - i // 计算天数间隔
        }
        
        // 当前索引入栈
        s = append(s, i) // 栈存储索引，而不是温度值
    }
    return res
}

BFS

773.滑动谜题

在一个 2 x 3 的板上（board）有 5 块砖瓦，用数字 1~5 来表示, 以及一块空缺用 0 来表示。一次移动定义为选择 0 与一个相邻的数字（上下左右）进行交换。

最终当板 board 的结果是 [[1,2,3],[4,5,0]] 谜板被解开。

给出一个谜板的初始状态 board，返回最少可以通过多少次移动解开谜板，如果不能解开谜板，则返回 -1。

示例 1：

输入：board = [[4,1,2],[5,0,3]]
输出：5
解释：
最少完成谜板的最少移动次数是 5 ，
一种移动路径:
尚未移动: [[4,1,2],[5,0,3]]
移动 1 次: [[4,1,2],[0,5,3]]
移动 2 次: [[0,1,2],[4,5,3]]
移动 3 次: [[1,0,2],[4,5,3]]
移动 4 次: [[1,2,0],[4,5,3]]
移动 5 次: [[1,2,3],[4,5,0]]

由于每一步操作等价于在图中搜索最短路径，最优解自然是 BFS：

将初始棋盘状态转换为字符串（例如 412503）。
使用队列 queue 进行 BFS：
- 每次弹出队列的当前状态，找到 0 的索引。
- 根据 0 在棋盘上的位置，确定它可以移动的方向（使用 dirs 数组）。
- 生成新状态，若未访问，则加入 queue。
- 如果生成的状态等于目标状态，直接返回步数。
使用 visited 集合去重，防止重复搜索。
若 queue 为空仍未找到目标状态，说明无解，返回 -1。

func slidingPuzzle(board [][]int) int {
    target := "123450"
    // 将 2x3 的数组转化成字符串作为 BFS 的起点
    start := ""
    for i := 0; i < len(board); i++ {
        for j := 0; j < len(board[0]); j++ {
            start += string(board[i][j] + '0')
        }
    }

    // ****** BFS 算法框架开始 ******
    queue := []string{start}
    visited := make(map[string]bool)
    visited[start] = true

    step := 0
    for len(queue) > 0 {
        sz := len(queue)
        for i := 0; i < sz; i++ {
            cur := queue[0]
            queue = queue[1:]
            // 判断是否达到目标局面
            if cur == target {
                return step
            }
            // 将数字 0 和相邻的数字交换位置
            for _, neighbor := range getNeighbors(cur) {
                // 防止走回头路
                if !visited[neighbor] {
                    queue = append(queue, neighbor)
                    visited[neighbor] = true
                }
            }
        }
        step++
    }
    // ****** BFS 算法框架结束 ******
    return -1
}

func getNeighbors(board string) []string {
    // 记录一维字符串的相邻索引
    mapping := [][]int{
        {1, 3},
        {0, 4, 2},
        {1, 5},
        {0, 4},
        {3, 1, 5},
        {4, 2},
    }

    idx := strings.Index(board, "0")
    neighbors := []string{}
    for _, adj := range mapping[idx] {
        newBoard := swap(board, idx, adj)
        neighbors = append(neighbors, newBoard)
    }
    return neighbors
}

func swap(board string, i, j int) string {
    chars := []rune(board)
    chars[i], chars[j] = chars[j], chars[i]
    return string(chars)
}

752.打开转盘锁

你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字：'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'。每个拨轮可以自由旋转：例如把 '9' 变为 '0'，'0' 变为 '9'。每次旋转都只能旋转一个拨轮的一位数字。

锁的初始数字为 '0000' ，一个代表四个拨轮的数字的字符串。

列表 deadends 包含了一组死亡数字，一旦拨轮的数字和列表里的任何一个元素相同，这个锁将会被永久锁定，无法再被旋转。

字符串 target 代表可以解锁的数字，你需要给出解锁需要的最小旋转次数，如果无论如何不能解锁，返回 -1。

示例 1:

输入：deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出：6
解释：
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的，
因为当拨动到 "0102" 时这个锁就会被锁定。

核心思路：

初始化：
- 使用一个哈希表 deads 来存储所有的死亡密码，方便快速查找。
- 使用另一个哈希表 visited 来记录已经访问过的密码，避免重复访问。
- 使用一个队列 q 来进行广度优先搜索，初始时将起点 "0000" 加入队列。
广度优先搜索（BFS）：
- 从队列中取出当前层的所有节点（密码），并尝试通过拨动密码锁的每一位（向上或向下）生成新的密码。
- 对于每一个新生成的密码，检查它是否是目标密码。如果是，返回当前的步数。
- 如果新密码不是死亡密码且没有被访问过，则将其加入队列，并标记为已访问。
- 每处理完一层节点（即当前队列中的所有节点），步数加一。
生成相邻密码：
- getNeighbors 函数用于生成当前密码的所有可能相邻密码。对于密码的每一位，分别向上拨动一次和向下拨动一次，共生成 8 种可能的相邻密码。
终止条件：
- 如果队列为空且没有找到目标密码，说明无法到达目标密码，返回 -1。

func openLock(deadends []string, target string) int {
    // 记录需要跳过的死亡密码
    deads := make(map[string]struct{})
    for _, s := range deadends {
        deads[s] = struct{}{}
    }
    if _, found := deads["0000"]; found {
        return -1
    }

    // 记录已经穷举过的密码，防止走回头路
    visited := make(map[string]struct{})
    q := make([]string, 0)
    // 从起点开始启动广度优先搜索
    step := 0
    q = append(q, "0000")
    visited["0000"] = struct{}{}
    
    for len(q) > 0 {
        sz := len(q)
        // 将当前队列中的所有节点向周围扩散
        for i := 0; i < sz; i++ {
            cur := q[0]
            q = q[1:]
            
            // 判断是否到达终点
            if cur == target {
                return step
            }
            
            // 将一个节点的合法相邻节点加入队列
            for _, neighbor := range getNeighbors(cur) {
                if _, found := visited[neighbor]; !found {
                    if _, dead := deads[neighbor]; !dead {
                        q = append(q, neighbor)
                        visited[neighbor] = struct{}{}
                    }
                }
            }
        }
        // 在这里增加步数
        step++
    }
    // 如果穷举完都没找到目标密码，那就是找不到了
    return -1
}

// 将 s[j] 向上拨动一次
func plusOne(s string, j int) string {
    ch := []rune(s)
    if ch[j] == '9' {
        ch[j] = '0'
    } else {
        ch[j]++
    }
    return string(ch)
}

// 将 s[i] 向下拨动一次
func minusOne(s string, j int) string {
    ch := []rune(s)
    if ch[j] == '0' {
        ch[j] = '9'
    } else {
        ch[j]--
    }
    return string(ch)
}

// 将 s 的每一位向上拨动一次或向下拨动一次，8 种相邻密码
func getNeighbors(s string) []string {
    neighbors := make([]string, 0)
    for i := 0; i < 4; i++ {
        neighbors = append(neighbors, plusOne(s, i))
        neighbors = append(neighbors, minusOne(s, i))
    }
    return neighbors
}

919.完全二叉树插入器

完全二叉树是每一层（除最后一层外）都是完全填充（即，节点数达到最大）的，并且所有的节点都尽可能地集中在左侧。

设计一种算法，将一个新节点插入到一棵完全二叉树中，并在插入后保持其完整。实现 CBTInserter 类:

CBTInserter(TreeNode root) 使用头节点为 root 的给定树初始化该数据结构；
CBTInserter.insert(int v) 向树中插入一个值为 Node.val == val 的新节点 TreeNode。使树保持完全二叉树的状态，并返回插入节点 TreeNode 的父节点的值；
CBTInserter.get_root() 将返回树的头节点。

核心思路：

CBTInserter（完全二叉树插入器）用于在完全二叉树中按照层序插入节点，同时保持其完全二叉树的性质。

1. 结构定义

q: 维护一个队列，仅存储当前二叉树底部 可以进行插入的节点（即至少有一个子节点为空）。
root: 指向二叉树的根节点。

2. 构造函数 (Constructor)

采用 广度优先遍历 (BFS) 遍历整棵树，找到所有可以插入的节点（即其 左或右子节点为空）。
这些节点存入 q，用于后续插入操作。

3. 插入 (Insert)

获取 q 中的队首节点 cur 作为父节点：
- 若 cur.Left 为空，则插入左子节点。
- 否则，插入右子节点，并 将 cur 出队，因为它的子节点已满。
新插入的节点同样可以接收新的子节点，因此 加入 q 队列。

4. 获取根节点 (Get_root)

直接返回 root，保证调用者可以访问整个二叉树。

type CBTInserter struct {
    // 这个队列只记录完全二叉树底部可以进行插入的节点
    q []*TreeNode
    root *TreeNode
}

func Constructor(root *TreeNode) CBTInserter {
    // 进行普通的 BFS，目的是找到底部可插入的节点
    q := []*TreeNode{}
    // temp 是为了遍历二叉树
    temp := []*TreeNode{root}
    for len(temp) > 0 {
        cur := temp[0]
        temp = temp[1:]
        if cur.Left != nil {
            temp = append(temp, cur.Left)
        }
        if cur.Right != nil {
            temp = append(temp, cur.Right)
        }
        if cur.Right == nil || cur.Left == nil {
            // 找到完全二叉树底部可以进行插入的节点
            q = append(q, cur)
        }
    }
    return CBTInserter{q: q, root: root}
}

func (this *CBTInserter) Insert(val int) int {
    node := &TreeNode{Val: val}
    cur := this.q[0]
    // 进行插入
    if cur.Left == nil {
        cur.Left = node
    } else if cur.Right == nil {
        cur.Right = node
        // 插入右子节点，并将 cur 出队，因为它的子节点已满。
        this.q = this.q[1:]
    }
    // 新节点的左右节点也是可以插入的
    this.q = append(this.q, node)
    return cur.Val
}

func (this *CBTInserter) Get_root() *TreeNode {
    return this.root
}

117.填充每个节点的下一个右侧节点指针 II

给定一个二叉树：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

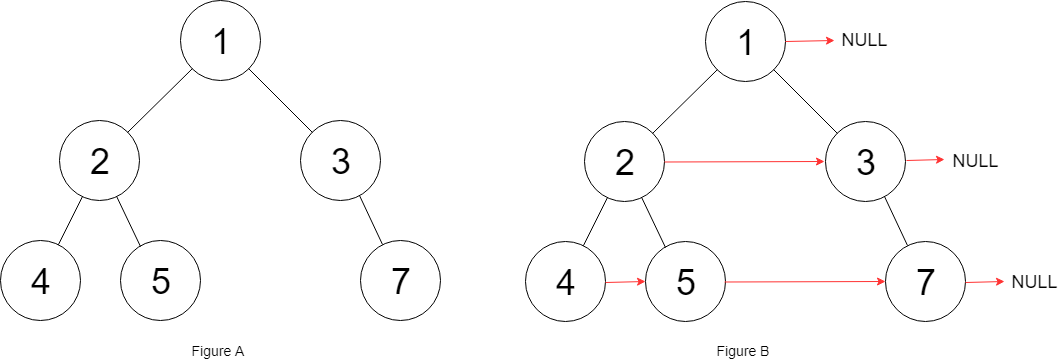
输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），'#' 表示每层的末尾。

这道题的目标是 填充二叉树中每个节点的 Next 指针，使其指向同一层的下一个右侧节点（如果没有则指向 nil）。

1. 层序遍历

采用 广度优先搜索 (BFS)，使用 队列 (queue) 逐层遍历二叉树。
每次处理当前层的所有节点，并确保 每个节点的 Next 指向它右侧的节点。

2. 处理 Next 指针

设当前层的节点数为 levelNum，遍历 i = 0 到 levelNum - 1：
- cur 为当前节点。
- 若 i < levelNum - 1，即当前节点不是这一层的最后一个节点，则令 cur.Next = queue[0]（即队列中的下一个节点）。
- 若 i == levelNum - 1，则 cur.Next 默认为 nil（无需额外操作）。

3. 入队下一层节点

若 cur 有 Left 子节点，则入队 queue。
若 cur 有 Right 子节点，则入队 queue。

4. 终止条件

queue 为空时，表示所有节点的 Next 指针已正确连接，返回 root。

func connect(root *Node) *Node {
    if root == nil {
        return nil // 空树直接返回
    }
    
    // 使用队列进行层序遍历（BFS）
    queue := []*Node{root}
    
    for len(queue) > 0 {
        levelNum := len(queue) // 记录当前层的节点数
        
        for i := 0; i < levelNum; i++ {
            cur := queue[0]  // 取出当前层的第一个节点
            queue = queue[1:] // 从队列中移除该节点
            
            // 连接当前节点的 Next 指针到右侧相邻节点（如果存在）
            if i < levelNum-1 {
                cur.Next = queue[0] // 当前节点指向队列中的下一个节点（即同层的下一个节点）
            }
            
            // 将下一层的节点加入队列
            if cur.Left != nil {
                queue = append(queue, cur.Left)
            }
            if cur.Right != nil {
                queue = append(queue, cur.Right)
            }
        }
    }
    
    return root // 返回修改后的树的根节点
}

662.二叉树最大宽度

给你一棵二叉树的根节点 root，返回树的最大宽度。

树的最大宽度是所有层中最大的宽度。

每一层的宽度被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

示例 1：

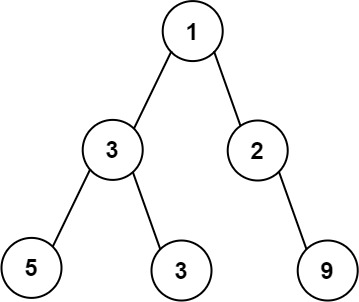
输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

核心思路：

层序遍历：使用队列来遍历每一层节点，同时记录每个节点的索引。
完全二叉树中，左子节点的索引为 2 × 当前节点索引。右子节点的索引为 2 × 当前节点索引 + 1。
计算每层宽度：每层宽度为最后一个节点索引减去第一个节点索引再加 1。

type NodeIndex struct {
    Node  *TreeNode
    Index int
}

func widthOfBinaryTree(root *TreeNode) int {
    if root == nil {
        return 0
    }

   // 使用队列保存节点和其索引，初始索引为 0
    queue := []NodeIndex{{Node: root, Index: 0}}
    maxWidth := 0

    for len(queue) > 0 {
        size := len(queue)
        
        // 计算每层的宽度，并与最大宽度进行比较
        levelStart, levelEnd := queue[0].Index, queue[len(queue)-1].Index
        maxWidth = max(maxWidth, levelEnd-levelStart+1)

        // 遍历当前层
        for i := 0; i < size; i++ {
            current := queue[0]
            queue = queue[1:]

            if current.Node.Left != nil {
                queue = append(queue, NodeIndex{Node: current.Node.Left, Index: 2 * current.Index})
            }
            if current.Node.Right != nil {
                queue = append(queue, NodeIndex{Node: current.Node.Right, Index: 2*current.Index + 1})
            }
        }
    }

    return maxWidth
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

863.二叉树中所有距离为 K 的结点

给定一个二叉树（具有根结点 root），一个目标结点 target ，和一个整数值 k，返回到目标结点 target 距离为 k 的所有结点的值的数组。

答案可以以任何顺序返回。

示例 1：

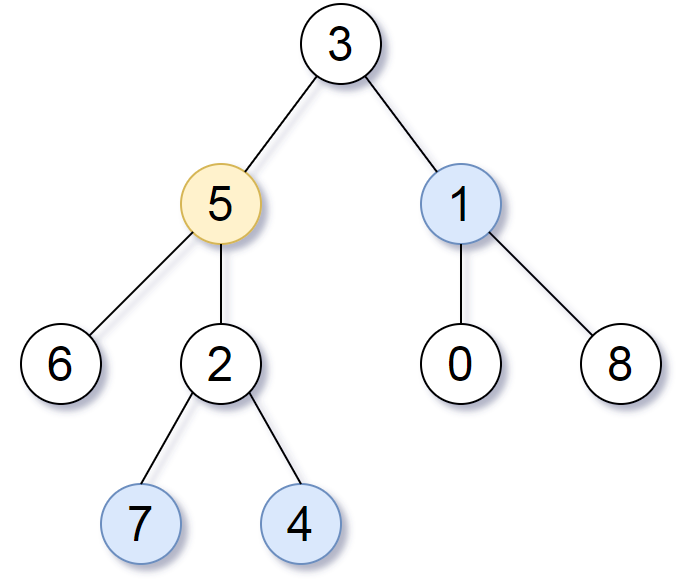
这道题的核心思路可以拆解为两个步骤：

遍历二叉树，记录每个节点的父节点（转化成无向图的一部分）
BFS 以目标 target 为起点，逐层扩展，找到所有距离 k 的节点

步骤 1：用 DFS 记录父节点

为什么要记录父节点？
- 在二叉树中，每个节点只有 左右子节点，但没有指向父节点的指针。
- 为了能从 target 反向遍历父节点，我们手动维护 parent 映射，记录每个节点的父节点。
实现方式
- 使用 DFS 遍历整棵树，把 node.Val -> parentNode 存到 parent map 里。
- 这样每个节点就有了双向关系，变成一个无向图结构，方便 BFS 遍历。

步骤 2：BFS 遍历 K 层

BFS 适用于层级遍历
- BFS 的本质是「逐层扩展」，我们从 target 开始扩展 K 层即可。
- 需要一个 队列 q，用于存储当前层的所有节点。
- 每一层遍历时：
  - 把 当前队列 q 里的所有节点 依次取出。
  - 把 所有未访问的相邻节点（父节点、左右子节点）加入 q。
  - 处理完当前层后，dist++ 记录层数。
- 当 dist == k 时，队列 q 里的所有节点就是答案。

func distanceK(root *TreeNode, target *TreeNode, k int) []int {
    // 记录父节点：node.val -> parentNode
    // 题目说了树中所有节点值都是唯一的，所以可以用 node.val 代表 TreeNode
    parent := make(map[int]*TreeNode)
    
    // 遍历所有节点，记录每个节点的父节点
    traverse(root, nil, parent)

    // 开始从 target 节点施放 BFS 算法，找到距离为 k 的节点
    q := []*TreeNode{target}
    visited := make(map[int]bool)
    visited[target.Val] = true
    // 记录离 target 的距离
    dist := 0
    var res []int

    for len(q) > 0 {
        if dist == k {
            // 找到距离起点 target 距离为 k 的节点
            for _, node := range q {
                res = append(res, node.Val)
            }
            return res
        }
        sz := len(q)
        for i := 0; i < sz; i++ {
            cur := q[0]
            q = q[1:]
            // 向父节点、左右子节点扩散
            if parentNode, ok := parent[cur.Val]; ok && parentNode != nil && !visited[parentNode.Val] {
                visited[parentNode.Val] = true
                q = append(q, parentNode)
            }
            if cur.Left != nil && !visited[cur.Left.Val] {
                visited[cur.Left.Val] = true
                q = append(q, cur.Left)
            }
            if cur.Right != nil && !visited[cur.Right.Val] {
                visited[cur.Right.Val] = true
                q = append(q, cur.Right)
            }
        }
        // 向外扩展一圈
        dist++
    }

    return res
}

func traverse(root *TreeNode, parentNode *TreeNode, parent map[int]*TreeNode) {
    if root == nil {
        return
    }
    parent[root.Val] = parentNode
    // 二叉树递归框架
    traverse(root.Left, root, parent)
    traverse(root.Right, root, parent)
}

841.钥匙和房间

有 n 个房间，房间按从 0 到 n - 1 编号。最初，除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而，你不能在没有获得钥匙的时候进入锁住的房间。

当你进入一个房间，你可能会在里面找到一套不同的钥匙，每把钥匙上都有对应的房间号，即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。

给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入所有房间返回 true，否则返回 false。

示例 1：

输入：rooms = [[1],[2],[3],[]]
输出：true
解释：
我们从 0 号房间开始，拿到钥匙 1。
之后我们去 1 号房间，拿到钥匙 2。
然后我们去 2 号房间，拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间，我们返回 true。

示例 2：

输入：rooms = [[1,3],[3,0,1],[2],[0]]
输出：false
解释：我们不能进入 2 号房间。

这道题可以用 DFS 或者 BFS 解决，代码如下：

// DFS 解法
func canVisitAllRooms(rooms [][]int) bool {
    n := len(rooms)
    visited := make([]bool, n)
    dfs(rooms, 0, visited)
    for _, v := range visited {
        if !v {
            return false
        }
    }
    return true
}

// 图的遍历框架
func dfs(rooms [][]int, room int, visited []bool) {
    if visited[room] {
        return
    }
    // 前序位置，标记房间已访问
    visited[room] = true

    for _, nextRoom := range rooms[room] {
        dfs(rooms, nextRoom, visited)
    }
}

// BFS 解法
func canVisitAllRooms2(rooms [][]int) bool {
    n := len(rooms)
    // 记录访问过的房间
    visited := make([]bool, n)
    queue := []int{0}
    // 在队列中加入起点，启动 BFS
    visited[0] = true

    for len(queue) > 0 {
        room := queue[0]
        queue = queue[1:]
        for _, nextRoom := range rooms[room] {
            if !visited[nextRoom] {
                visited[nextRoom] = true
                queue = append(queue, nextRoom)
            }
        }
    }

    for _, v := range visited {
        if !v {
            return false
        }
    }
    return true
}

1306.跳跃游戏 III

这里有一个非负整数数组 arr，你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时，你可以跳到 i + arr[i] 或者 i - arr[i]。

请你判断自己是否能够跳到对应元素值为 0 的任一下标处。

注意，不管是什么情况下，你都无法跳到数组之外。

示例 1：

输入：arr = [4,2,3,0,3,1,2], start = 5
输出：true
解释：
到达值为 0 的下标 3 有以下可能方案： 
下标 5 -> 下标 4 -> 下标 1 -> 下标 3 
下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3

核心思路：

使用 BFS 进行层序遍历
- 把 start 放入队列 q 作为搜索的起点。
- 每次取出队列中的元素 cur，尝试跳到 cur - arr[cur]（左）和 cur + arr[cur]（右）。
- 如果 arr[cur] == 0，说明找到目标，返回 true。
用 visited 数组避免重复访问
- 避免陷入死循环（如 [4,2,3,0,3,1,2]，arr[0] = 4，可能反复跳 0 → 4 → 0 → 4）。
- 每访问一个新位置，就标记 visited，防止重复搜索。
BFS 终止条件
- 找到 arr[i] == 0，直接返回 true。
- 队列 q 为空，表示所有可达位置都搜索完了，仍然找不到 0，返回 false。

func canReach(arr []int, start int) bool {
    visited := make([]bool, len(arr))
    q := []int{start}
    visited[start] = true
    // 标准 BFS 算法框架
    for len(q) > 0 {
        cur := q[0]
        q = q[1:]
        if arr[cur] == 0 {
            return true
        }
        // 往左跳
        left := cur - arr[cur]
        if left >= 0 && !visited[left] {
            q = append(q, left)
            visited[left] = true
        }
        // 往右跳
        right := cur + arr[cur]
        if right < len(arr) && !visited[right] {
            q = append(q, right)
            visited[right] = true
        }
    }
    return false
}

433.最小基因变化

基因序列可以表示为一条由 8 个字符组成的字符串，其中每个字符都是 'A'、'C'、'G' 和 'T' 之一。

假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。

例如，"AACCGGTT" --> "AACCGGTA" 就是一次基因变化。

另有一个基因库 bank 记录了所有有效的基因变化，只有基因库中的基因才是有效的基因序列。（变化后的基因必须位于基因库 bank 中）

给你两个基因序列 start 和 end，以及一个基因库 bank，请你找出并返回能够使 start 变化为 end 所需的最少变化次数。如果无法完成此基因变化，返回 -1。

注意：起始基因序列 start 默认是有效的，但是它并不一定会出现在基因库中。

示例 1：

输入：start = "AACCGGTT", end = "AACCGGTA", bank = ["AACCGGTA"]
输出：1

示例 2：

输入：start = "AACCGGTT", end = "AAACGGTA", bank = ["AACCGGTA","AACCGCTA","AAACGGTA"]
输出：2

示例 3：

输入：start = "AAAAACCC", end = "AACCCCCC", bank = ["AAAACCCC","AAACCCCC","AACCCCCC"]
输出：3

核心思路：

构建基因库集合 (bankSet)
- 使用 map[string]struct{} 存储 bank 中的基因，提高查询效率 (O(1))。
- 如果 endGene 不在 bankSet 中，则直接返回 -1，因为无法变异到目标基因。
广度优先搜索（BFS）求最短路径
- 初始化队列 (q)，将 startGene 作为起点，并标记为访问过 (visited)。
- 逐层扩展，每次遍历当前队列中的所有基因：
  - 如果当前基因 cur 等于 endGene，返回当前步数 step。
  - 计算 cur 的所有可能变异 (getAllMutation)，如果新基因在 bankSet 中且未访问，则加入队列并标记已访问。
- 步数累加，每遍历完一层，步数 step++，直到队列为空仍未找到 endGene，则返回 -1。
计算所有可能的变异 (getAllMutation)
- 遍历 gene 的每个位置，尝试用 A/G/C/T 替换原字符，生成所有可能的变异基因。
- 过滤掉 startGene 本身（即变异字符不能和原字符相同）。
- 返回所有可能的新基因列表，用于 BFS 进一步扩展。

func minMutation(startGene string, endGene string, bank []string) int {
    // 使用 map 存储 bank 中的基因，方便根据基因判断是否存在
    bankSet := make(map[string]struct{})
    for _, gene := range bank {
        bankSet[gene] = struct{}{}
    }
    if _, exists := bankSet[endGene]; !exists {
        return -1
    }

    // BFS 标准框架
    q := []string{startGene}
    visited := make(map[string]bool)
    visited[startGene] = true
    step := 0
    for len(q) > 0 {
        sz := len(q)
        for j := 0; j < sz; j++ {
            cur := q[0]
            q = q[1:]
            if cur == endGene {
                return step
            }
            // 向周围扩散
            for _, newGene := range getAllMutation(cur) {
                if _, seen := visited[newGene]; !seen {
                    if _, valid := bankSet[newGene]; valid {
                        q = append(q, newGene)
                        visited[newGene] = true
                    }
                }
            }
        }
        step++
    }
    return -1
}

// 当前基因的每个位置都可以变异为 A/G/C/T，穷举所有可能的结构
func getAllMutation(gene string) []string {
    res := []string{}
    geneChars := []rune(gene)
    for i := 0; i < len(geneChars); i++ {
        oldChar := geneChars[i]
        for _, newChar := range []rune{'A', 'G', 'C', 'T'} {
            if newChar != oldChar {
                geneChars[i] = newChar
                res = append(res, string(geneChars))
            }
        }
        // 恢复原始基因字符串，防止影响后续的变异计算
        geneChars[i] = oldChar
    }
    return res
}

1926.迷宫中离入口最近的出口

给你一个 m x n 的迷宫矩阵 maze（下标从 0 开始），矩阵中有空格子（用 '.' 表示）和墙（用 '+' 表示）。同时给你迷宫的入口 entrance，用 entrance = [entrancerow, entrancecol] 表示你一开始所在格子的行和列。

每一步操作，你可以往上，下，左或者右移动一个格子。你不能进入墙所在的格子，你也不能离开迷宫。你的目标是找到离 entrance 最近的出口。出口的含义是 maze 边界上的空格子。entrance 格子不算出口。

请你返回从 entrance 到最近出口的最短路径的步数，如果不存在这样的路径，请你返回 -1。

核心思路：

使用 BFS 进行最短路径搜索
- 迷宫是 网格（二维数组），从 entrance 开始，寻找 最近的出口。
- BFS 适用于最短路径问题，因为它逐层扩展，最早到达的出口必然是最短路径。
如何判断出口？
- 迷宫出口必须是边界上的 .。
- 不能是 entrance 本身（即 entrance 不能算作出口）。
BFS 遍历方式
- 初始化 BFS 队列，从 entrance 开始。
- 每次从队列取出一个位置，尝试向 上、下、左、右 四个方向扩展。
- 遇到出口立即返回当前步数，因为 BFS 先找到的一定是最近的出口。
避免重复访问
- 用 visited 数组 记录已访问位置，防止死循环。

// BFS 算法的队列和 visited 数组
func nearestExit(maze [][]byte, entrance []int) int {
    m := len(maze)
    n := len(maze[0])
    dirs := [][]int{{0, 1}, {0, -1}, {1, 0}, {-1, 0}}
    
    queue := make([][]int, 0)
    visited := make([][]bool, m)
    for i := range visited {
        visited[i] = make([]bool, n)
    }
    
    queue = append(queue, entrance)
    visited[entrance[0]][entrance[1]] = true
    
    // 启动 BFS 算法从 entrance 开始像四周扩散
    step := 0
    for len(queue) > 0 {
        sz := len(queue)
        step++
        // 扩散当前队列中的所有节点
        for i := 0; i < sz; i++ {
            cur := queue[0]
            queue = queue[1:]
            // 每个节点都会尝试向上下左右四个方向扩展一步
            for _, dir := range dirs {
                x := cur[0] + dir[0]
                y := cur[1] + dir[1]
                if x < 0 || x >= m || y < 0 || y >= n || visited[x][y] || maze[x][y] == '+' {
                    continue
                }
                if x == 0 || x == m-1 || y == 0 || y == n-1 {
                    // 走到边界（出口）
                    return step
                }
                visited[x][y] = true
                queue = append(queue, []int{x, y})
            }
        }
    }
    return -1
}

1091.二进制矩阵中的最短路径

给你一个 n x n 的二进制矩阵 grid 中，返回矩阵中最短畅通路径的长度。如果不存在这样的路径，返回 -1。

二进制矩阵中的畅通路径是一条从左上角单元格（即，(0, 0)）到右下角单元格（即，(n - 1, n - 1)）的路径，该路径同时满足下述要求：

路径途经的所有单元格的值都是 0。
路径中所有相邻的单元格应当在 8 个方向之一上连通（即，相邻两单元之间彼此不同且共享一条边或者一个角）。
畅通路径的长度是该路径途经的单元格总数。

示例 1：

输入：grid = [[0,1],[1,0]]
输出：2

示例 2：

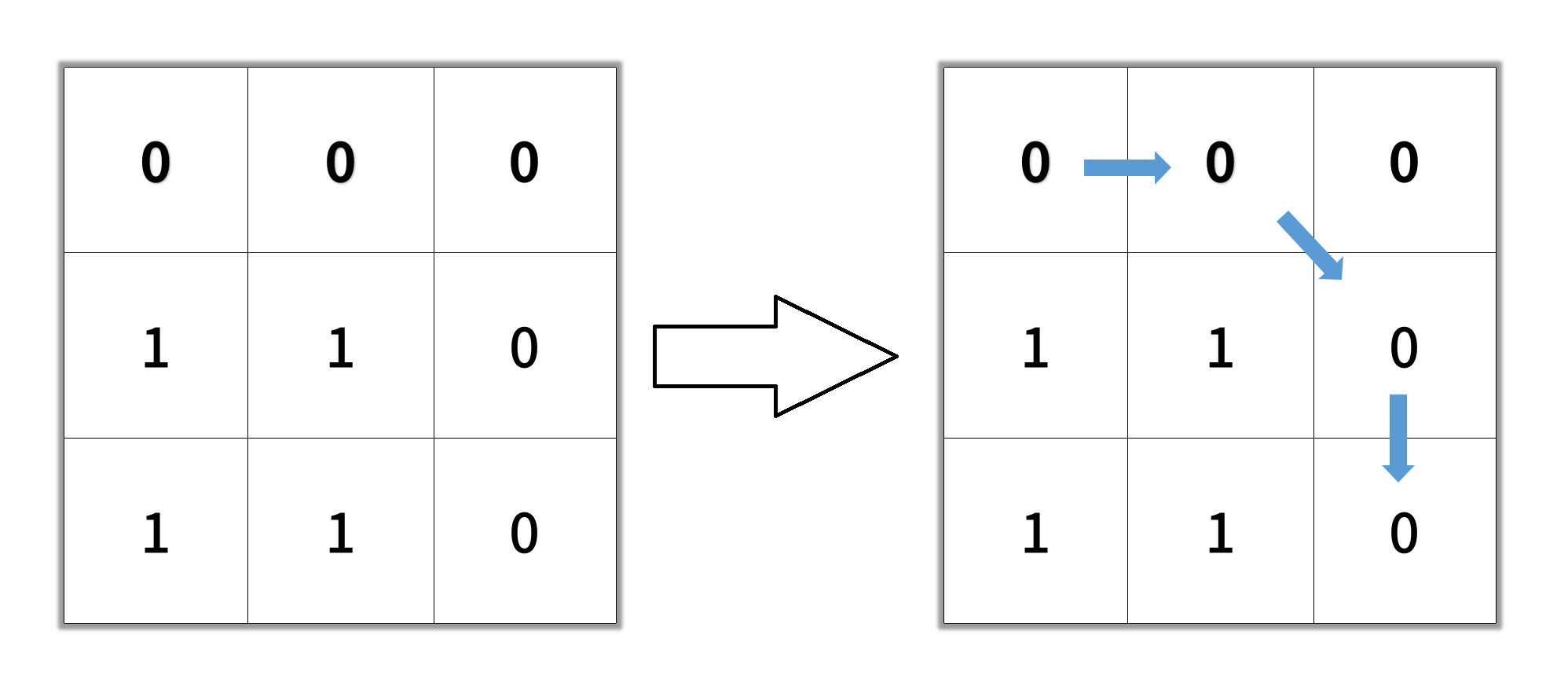
输入：grid = [[0,0,0],[1,1,0],[1,1,0]]
输出：4

示例 3：

输入：grid = [[1,0,0],[1,1,0],[1,1,0]]
输出：-1

核心思路：

使用 BFS（广度优先搜索）找最短路径
- 由于每次只能走到相邻的 0，并且路径的步数是单位步长，使用 BFS 可以保证找到的路径是最短的。
特殊情况判断
- 如果起点 (0,0) 或终点 (m-1,n-1) 是 1（障碍物），直接返回 -1，因为无法出发或无法抵达。
BFS 过程
- 初始化 BFS 队列，从起点 (0,0) 开始，并标记已访问。
- 逐层扩展，每次从 queue 取出当前层的所有节点，向 8 个方向 扩展。
- 如果某个节点 (m-1, n-1) 被访问到，立即返回当前步数，因为 BFS 保证最早到达的路径是最短路径。
访问控制
- 使用 visited 数组 记录访问过的节点，避免重复访问。
- 边界检查，确保新的坐标在 grid 范围内，且是 0（可走路径）。
无法到达目标
- 如果 BFS 结束后仍然没有访问到终点，返回 -1，表示无法找到通往终点的路径。

func shortestPathBinaryMatrix(grid [][]int) int {
    m, n := len(grid), len(grid[0]) // 获取网格的行数和列数
    
    // 如果起点 (0,0) 或终点 (m-1,n-1) 是障碍物，无法通行，直接返回 -1
    if grid[0][0] == 1 || grid[m-1][n-1] == 1 {
        return -1
    }

    // 记录访问过的格子，防止重复搜索
    visited := make([][]bool, m)
    for i := range visited {
        visited[i] = make([]bool, n)
    }

    // 8 个方向的移动方式（上下左右+四个对角线）
    dirs := [][]int{
        {0, 1},  {0, -1},  {1, 0},  {-1, 0}, 
        {1, 1},  {1, -1},  {-1, 1}, {-1, -1},
    }

    // BFS 队列初始化，存储 {x, y} 位置
    queue := make([][]int, 0)
    queue = append(queue, []int{0, 0}) // 将起点 (0,0) 入队
    visited[0][0] = true // 标记起点已访问

    step := 1 // 记录当前的步数，从 1 开始（因为起点本身算一步）
    
    // 开始 BFS 搜索
    for len(queue) > 0 {
        sz := len(queue) // 当前层的节点数
        
        // 遍历当前层的所有节点
        for i := 0; i < sz; i++ {
            cur := queue[0]   // 取出队列头部的节点
            queue = queue[1:] // 出队列

            x, y := cur[0], cur[1] // 当前所在位置

            // 如果到达终点 (m-1, n-1)，返回步数
            if x == m-1 && y == n-1 {
                return step
            }

            // 遍历 8 个方向，扩展下一层
            for _, dir := range dirs {
                nextX := x + dir[0]
                nextY := y + dir[1]

                // 边界检查 + 未访问 + 不能是障碍物
                if nextX < 0 || nextX >= m || nextY < 0 || nextY >= n || visited[nextX][nextY] || grid[nextX][nextY] == 1 {
                    continue
                }

                // 标记该位置已访问，并加入队列
                visited[nextX][nextY] = true
                queue = append(queue, []int{nextX, nextY})
            }
        }
        step++ // 每遍历完一层，步数加一
    }

    // 如果 BFS 结束后仍然没有到达终点，返回 -1
    return -1
}

310.最小高度树

树是一个无向图，其中任何两个顶点只通过一条路径连接。换句话说，任何一个没有简单环路的连通图都是一棵树。

给你一棵包含 n 个节点的树，标记为 0 到 n - 1。给定数字 n 和一个有 n - 1 条无向边的 edges 列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。

可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h。在所有可能的树中，具有最小高度的树（即，min(h)）被称为最小高度树。

请你找到所有的最小高度树并按任意顺序返回它们的根节点标签列表。

树的高度是指根节点和叶子节点之间最长向下路径上边的数量。

示例 1：

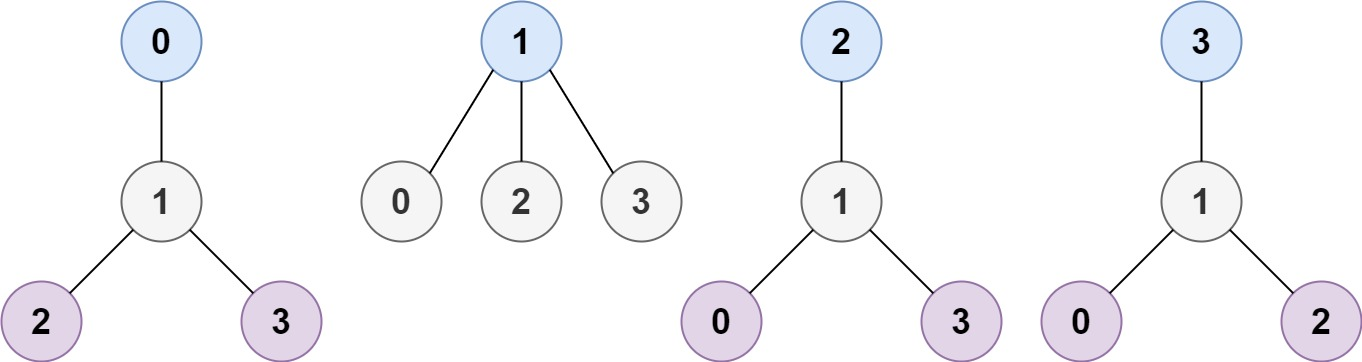
输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。

示例 2：

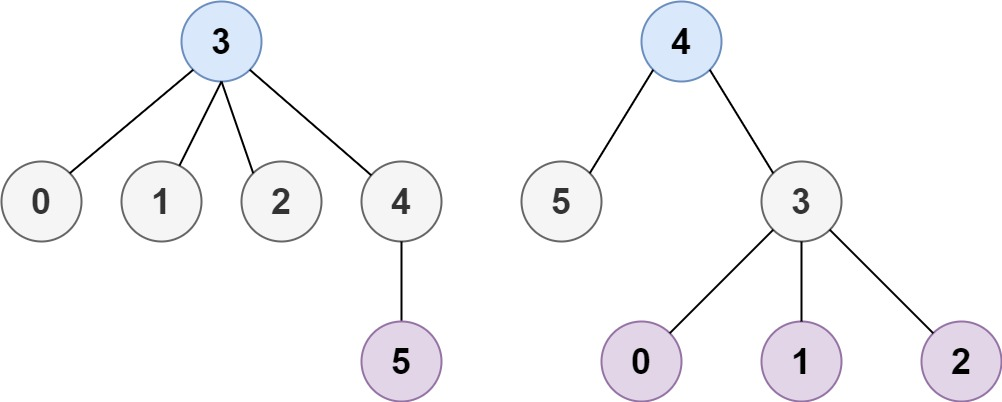
输入：n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出：[3,4]

核心思路：

1. 首先，我们把题目输入的 edges 转换成邻接表。
1. 然后，我们从叶子节点开始，一层一层地删除叶子节点（每删除一层叶子节点，就会产生新的叶子节点），直到剩下的节点数小于等于 2 个为止。之所以是 2 个而不是 1 个，是因为如果输入的这幅图两边完全对称，可能出现两个节点都可以作为根节点的情况。

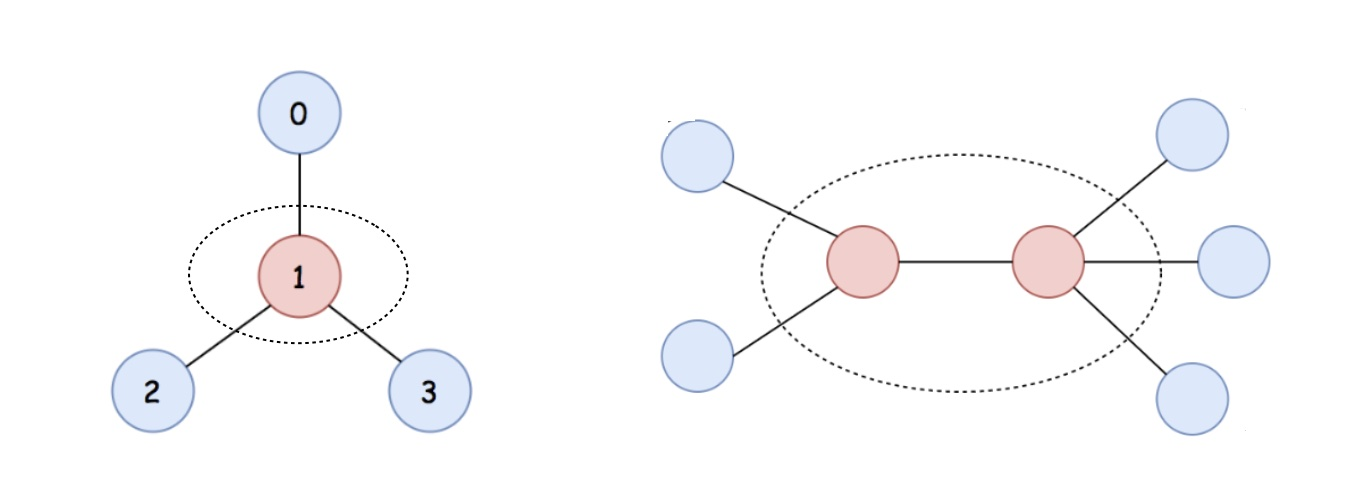
3.最后剩下的这些节点，就是我们要找的最小高度树的根节点。

func findMinHeightTrees(n int, edges [][]int) []int {
    if n == 1 {
        // base case，只有一个节点 0 的话，无法形成边，所以直接返回节点 0
        return []int{0}
    }

    // 1、构建邻接表
    graph := make([][]int, n)
    for i := 0; i < n; i++ {
        graph[i] = []int{}
    }
    for _, edge := range edges {
        // 无向图，等同于双向图
        graph[edge[0]] = append(graph[edge[0]], edge[1])
        graph[edge[1]] = append(graph[edge[1]], edge[0])
    }

    // 2、找到所有的叶子节点
    q := []int{}
    for i := 0; i < n; i++ {
        if len(graph[i]) == 1 {
            q = append(q, i)
        }
    }

    // 3、不断删除叶子节点，直到剩下的节点数小于等于 2 个
    nodeCount := n
    for nodeCount > 2 {
        sz := len(q)
        nodeCount -= sz
        newQ := []int{}
        for i := 0; i < sz; i++ {
            // 删除当前叶子节点
            cur := q[i]

            // 找到与当前叶子节点相连的节点
            for _, neighbor := range graph[cur] {
                // 将被删除的叶子节点的邻接节点的度减 1
                for j, val := range graph[neighbor] {
                    if val == cur {
                        graph[neighbor] = append(graph[neighbor][:j], graph[neighbor][j+1:]...)
                    }
                }

                // 如果删除后，相连节点的度为 1，说明它也变成了叶子节点
                if len(graph[neighbor]) == 1 {
                    newQ = append(newQ, neighbor)
                }
            }
        }
        q = newQ
    }

    // 4、最后剩下的节点就是根节点
    return q
}

算法解题套路框架 ​

回溯 ​

模板 ​

例题 ​

78.子集（元素无重不可复选） ​

77.组合（元素无重不可复选） ​

216.组合总和 III（元素无重不可复选） ​

46.全排列（元素无重不可复选） ​

90.子集 II（元素可重不可复选） ​

40.组合总和 II（元素可重不可复选） ​

47.全排列 II（元素可重不可复选） ​

39.组合总和（元素无重可复选） ​

22.括号生成 ​

698. 划分为k个相等的子集 ​

数组 ​

快慢指针 ​

原地修改 ​

26. 删除有序数组中的重复项 ​

27. 移除元素 ​

滑动窗口 ​

模板 ​

例题 ​

76.最小覆盖子串 ​

567.字符串的排列 ​

438.找到字符串中所有字母异位词 ​

4.最长无重复子串 ​

左右指针 ​

二分查找 ​

n 数之和 ​

1.两数之和 ​

15.三数之和 ​

18.四数之和 ​

反转数组 ​

344.反转字符串 ​

回文串判断 ​

5.最长回文子串 ​

二维数组遍历 ​

顺/逆时针旋转矩阵 ​

矩阵的螺旋遍历 ​

54.螺旋矩阵 ​

59.螺旋矩阵 II ​

前缀和 ​

差分数组 ​

栈 ​

单调栈 ​

BFS ​

算法解题套路框架

回溯

模板

例题

78.子集（元素无重不可复选）

77.组合（元素无重不可复选）

216.组合总和 III（元素无重不可复选）

46.全排列（元素无重不可复选）

90.子集 II（元素可重不可复选）

40.组合总和 II（元素可重不可复选）

47.全排列 II（元素可重不可复选）

39.组合总和（元素无重可复选）

22.括号生成

698. 划分为k个相等的子集

数组

快慢指针

原地修改

26. 删除有序数组中的重复项

27. 移除元素

滑动窗口

模板

例题

76.最小覆盖子串

567.字符串的排列

438.找到字符串中所有字母异位词

4.最长无重复子串

左右指针

二分查找

n 数之和

1.两数之和

15.三数之和

18.四数之和

反转数组

344.反转字符串

回文串判断

5.最长回文子串

二维数组遍历

顺/逆时针旋转矩阵

矩阵的螺旋遍历

54.螺旋矩阵

59.螺旋矩阵 II

前缀和

差分数组

栈

单调栈

BFS