Se7en的架构笔记

LRU 缓存

请你设计并实现一个满足 LRU (最近最少使用) 缓存约束的数据结构。

实现 LRUCache 类：

LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value；如果不存在，则向缓存中插入该组 key-value。如果插入操作导致关键字数量超过 capacity ，则应该逐出最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：


输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

题解

1.首先，题目中提到函数 get 和 put 必须以 O(1) 的平均时间复杂度运行，很自然地我们可以想到应该使用哈希表。
2.其次，当访问数据结构中的某个 key 时，需要将这个 key 更新为最近使用；另外如果 capacity 已满，需要删除访问时间最早的那条数据。这要求数据是有序的，并且可以支持在任意位置快速插入和删除元素，链表可以满足这个要求。
3.结合 1，2 两点来看，我们可以采用哈希表 + 链表的结构实现 LRU 缓存。

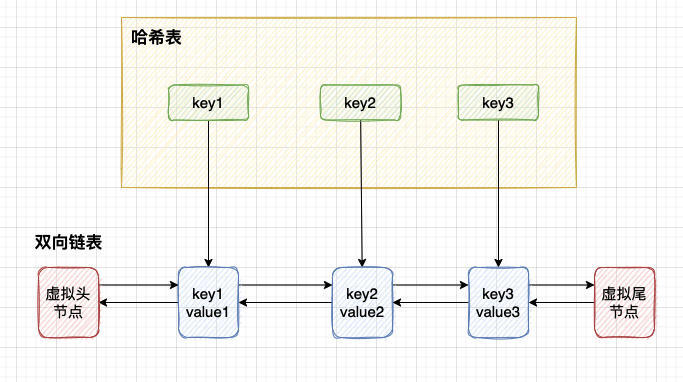
package main

import "fmt"

// LRU 数据结构
type LRUCache struct {
	capacity   int                  // 容量
	size       int                  // 已使用空间
	head, tail *DLinkedNode         // 头节点，尾节点
	cache      map[int]*DLinkedNode // 哈希表
}

// 双向链表数据结构
type DLinkedNode struct {
	key, value int
	prev, next *DLinkedNode // 前指针，后指针
}

// 创建一个新的节点
func initDLinkedNode(key, value int) *DLinkedNode {
	return &DLinkedNode{
		key:   key,
		value: value,
	}
}

// 初始化 LRU 结构
func Constructor(capacity int) LRUCache {
	l := LRUCache{
		cache:    map[int]*DLinkedNode{}, //  哈希表
		head:     initDLinkedNode(0, 0),  // 虚拟头节点
		tail:     initDLinkedNode(0, 0),  // 虚拟尾节点
		capacity: capacity,               // 容量
	}
	// 虚拟头节点和虚拟尾节点互连
	l.head.next = l.tail
	l.tail.prev = l.head
	return l
}

// 获取元素
func (this *LRUCache) Get(key int) int {
	// 如果没有在哈希表中找到 key
	if _, ok := this.cache[key]; !ok {
		return -1
	}
	// 如果 key 存在，先通过哈希表定位，再移到头部
	node := this.cache[key]
	this.moveToHead(node)
	return node.value
}

// 插入元素
func (this *LRUCache) Put(key int, value int) {
	// 先去哈希表中查询
	// 如果 key 不存在，创建一个新的节点
	if node, ok := this.cache[key]; !ok {
		newNode := initDLinkedNode(key, value)
		// 如果达到容量限制，链表删除尾部节点，哈希表删除元素
		this.size++
		if this.size > this.capacity {
			// 得到删除的节点
			removed := this.removeTail()
			// 根据得到的 key 删除哈希表中的元素
			delete(this.cache, removed.key)
			// 减少已使用容量
			this.size--
		}
		// 插入哈希表
		this.cache[key] = newNode
		// 插入链表
		this.addToHead(newNode)
	} else { // 如果 key 存在，先通过哈希表定位，再修改 value，并移到头部
		node.value = value
		this.moveToHead(node)
	}
}

// 将节点添加到头部
func (this *LRUCache) addToHead(node *DLinkedNode) {
	// 新节点指向前后节点
	node.prev = this.head
	node.next = this.head.next
	
	// 前后节点指向新节点
	this.head.next.prev = node
	this.head.next = node
}

// 删除该节点
func (this *LRUCache) removeNode(node *DLinkedNode) {
	// 修改该节点前后节点的指针，不再指向该节点
	node.next.prev = node.prev
	node.prev.next = node.next
}

// 移动到头部，也就是当前位置删除，再添加到头部
func (this *LRUCache) moveToHead(node *DLinkedNode) {
	this.removeNode(node)
	this.addToHead(node)
}

// 移除尾部节点，淘汰最久未使用的
func (this *LRUCache) removeTail() *DLinkedNode {
	node := this.tail.prev // 虚拟尾节点的上一个才是真正的尾节点
	this.removeNode(node)
	return node
}

LFU 缓存

请你为最不经常使用（LFU）缓存算法设计并实现数据结构。

实现 LFUCache 类：

LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象。
int get(int key) - 如果键 key 存在于缓存中，则获取键的值，否则返回 -1 。
void put(int key, int value) - 如果键 key 已存在，则变更其值；如果键不存在，请插入键值对。当缓存达到其容量 capacity 时，则应该在插入新项之前，移除最不经常使用的项。在此问题中，当存在平局（即两个或更多个键具有相同使用频率）时，应该去除最久未使用的键。

为了确定最不常使用的键，可以为缓存中的每个键维护一个使用计数器。使用计数最小的键是最久未使用的键。

当一个键首次插入到缓存中时，它的使用计数器被设置为 1 (由于 put 操作)。对缓存中的键执行 get 或 put 操作，使用计数器的值将会递增。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入：
["LFUCache", "put", "put", "get", "put", "get", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [3], [4, 4], [1], [3], [4]]
输出：
[null, null, null, 1, null, -1, 3, null, -1, 3, 4]

解释：
// cnt(x) = 键 x 的使用计数
// cache=[] 将显示最后一次使用的顺序（最左边的元素是最近的）
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1);   // cache=[1,_], cnt(1)=1
lfu.put(2, 2);   // cache=[2,1], cnt(2)=1, cnt(1)=1
lfu.get(1);      // 返回 1
                 // cache=[1,2], cnt(2)=1, cnt(1)=2
lfu.put(3, 3);   // 去除键 2 ，因为 cnt(2)=1 ，使用计数最小
                 // cache=[3,1], cnt(3)=1, cnt(1)=2
lfu.get(2);      // 返回 -1（未找到）
lfu.get(3);      // 返回 3
                 // cache=[3,1], cnt(3)=2, cnt(1)=2
lfu.put(4, 4);   // 去除键 1 ，1 和 3 的 cnt 相同，但 1 最久未使用
                 // cache=[4,3], cnt(4)=1, cnt(3)=2
lfu.get(1);      // 返回 -1（未找到）
lfu.get(3);      // 返回 3
                 // cache=[3,4], cnt(4)=1, cnt(3)=3
lfu.get(4);      // 返回 4
                 // cache=[3,4], cnt(4)=2, cnt(3)=3

题解

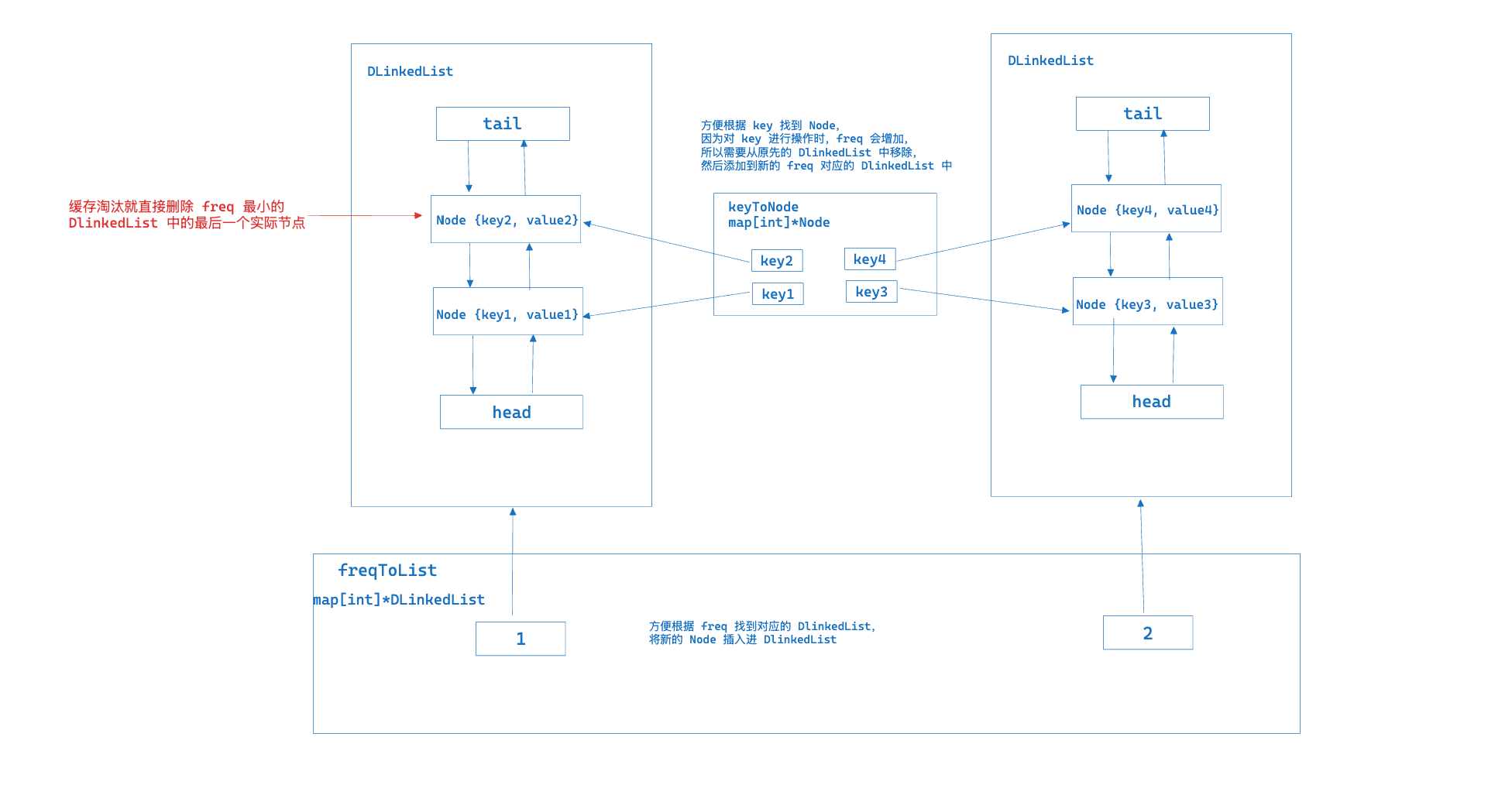
type Node struct {
    key, value, freq int
    prev, next *Node
}

type DLinkedList struct {
    head, tail *Node
    size       int
}

func newDLinkedList() *DLinkedList {
    list := &DLinkedList{
        head: &Node{},
        tail: &Node{},
    }
    list.head.next = list.tail
    list.tail.prev = list.head
    return list
}

func (l *DLinkedList) addNode(node *Node) {
    node.prev = l.head
    node.next = l.head.next
    l.head.next.prev = node
    l.head.next = node
    l.size++
}

func (l *DLinkedList) removeNode(node *Node) {
    node.prev.next = node.next
    node.next.prev = node.prev
    l.size--
}

func (l *DLinkedList) removeLast() *Node {
    if l.size > 0 {
        lastNode := l.tail.prev
        l.removeNode(lastNode)
        return lastNode
    }
    return nil
}

type LFUCache struct {
    capacity    int
    size        int
    minFreq     int
    keyToNode   map[int]*Node
    freqToList  map[int]*DLinkedList
}

func Constructor(capacity int) LFUCache {
    return LFUCache{
        capacity:   capacity,
        keyToNode:  make(map[int]*Node),
        freqToList: make(map[int]*DLinkedList),
    }
}

func (c *LFUCache) updateFreq(node *Node) {
    // 从原频率链表中删除
    freq := node.freq
    c.freqToList[freq].removeNode(node)
    
    // 如果当前频率的链表为空且是最小频率，更新最小频率
    if c.minFreq == freq && c.freqToList[freq].size == 0 {
        c.minFreq++
    }
    
    // 将节点加入新频率的链表
    node.freq++
    if _, ok := c.freqToList[node.freq]; !ok {
        c.freqToList[node.freq] = newDLinkedList()
    }
    c.freqToList[node.freq].addNode(node)
}

func (c *LFUCache) Get(key int) int {
    if node, ok := c.keyToNode[key]; ok {
        c.updateFreq(node)
        return node.value
    }
    return -1
}

func (c *LFUCache) Put(key int, value int) {
    if c.capacity == 0 {
        return
    }
    
    // 如果键已存在，更新值和频率
    if node, ok := c.keyToNode[key]; ok {
        node.value = value
        c.updateFreq(node)
        return
    }
    
    // 如果缓存已满，删除使用频率最小的元素中最久未使用的那个
    if c.size >= c.capacity {
        minFreqList := c.freqToList[c.minFreq]
        deletedNode := minFreqList.removeLast()
        delete(c.keyToNode, deletedNode.key)
        c.size--
    }
    
    // 插入新节点
    newNode := &Node{key: key, value: value, freq: 1}
    c.keyToNode[key] = newNode
    if _, ok := c.freqToList[1]; !ok {
        c.freqToList[1] = newDLinkedList()
    }
    c.freqToList[1].addNode(newNode)
    c.minFreq = 1
    c.size++
}

带权随机选择

带权随机选择(Weighted Random) 的核心是：根据每个对象的权重进行概率性地选择。权重越大，被选中的概率越高。实现方式通常分为两步：

计算所有对象的权重和 totalWeight。
从区间 [0, totalWeight) 中随机生成一个值 r，然后遍历所有对象的权重累加值，一旦累加值超过 r，就返回该对象。
每次都用随机数落在 [0, totalWeight) 区间，根据累加判断选中谁，短期内有随机波动。

package main

import (
	"fmt"
	"math/rand"
	"time"
)

// WeightedItem 用来表示带权的对象
type WeightedItem struct {
	Value  string
	Weight int
}

// WeightedRandom 从给定的 weightedItems 中，随机返回一个对象
func WeightedRandom(weightedItems []WeightedItem) *WeightedItem {
	if len(weightedItems) == 0 {
		return nil
	}
	// 计算权重总和
	totalWeight := 0
	for _, item := range weightedItems {
		totalWeight += item.Weight
	}

	// 在 [0, totalWeight) 区间内取随机数
	r := rand.Intn(totalWeight)

	// 遍历找到对应区间的对象
	cumulative := 0
	for _, item := range weightedItems {
		cumulative += item.Weight
		if r < cumulative {
			return &item
		}
	}

	return nil
}

func main() {
	rand.Seed(time.Now().UnixNano()) // 初始化随机种子

	items := []WeightedItem{
		{Value: "A", Weight: 1},
		{Value: "B", Weight: 2},
		{Value: "C", Weight: 5},
	}

	// 统计多次测试的分布
	count := map[string]int{}
	for i := 0; i < 100; i++ {
		sel := WeightedRandom(items)
		fmt.Print(sel.Value)
		count[sel.Value]++
	}

	fmt.Println("\nCount Distribution:", count)
}


// 输出结果
// AACBCBCCCCBCBCCAACBCCCBACBCAACCCBBCCCCCCBCCCCCCCCCCCCCBCCCCCCCBCBCCBBACABCCCCCCBCBBABBAABABCCCCCCBCA
// Count Distribution: map[A:14 B:24 C:62]

平滑加权轮询

在平滑加权轮询（Smooth Weighted Round Robin）算法里，维护一个 currentWeight（有时也称“当前负载”或“当前权重”）是实现“平滑”效果的关键所在。它的作用主要有以下几点：

逐步累加、确保“饿”的节点能被选中：
- 每轮调度前，会对每个节点的 currentWeight 加上它的静态 Weight。
- 如果某个节点好几轮都没被选中，那么它的 currentWeight 将持续累加、不断增大。这样一来，它就能“追赶”或超过其他节点的 currentWeight，从而在下一轮调度时被选中。这种逻辑可以理解为“节点越久没被选中，下次优先级会越高”，有助于更平滑、均衡地分配。
被选中的节点要减去 totalWeight，避免一直占优：
- 当某个节点被选中后，会把它的 currentWeight 减去所有节点权重之和 totalWeight。
- 这样能防止同一个节点连续被选中过多次：它刚被选中时“消耗”了大量当前权重，自然就要让其他节点有机会（因为其他节点每轮都会持续加它们自己的权重）。

package main

import (
	"fmt"
)

// WeightedItem 表示一个带有权重的元素
type WeightedItem struct {
	Value         string // 元素标识（比如服务器地址等）
	Weight        int    // 静态配置的权重
	currentWeight int    // 动态“当前权重”，用于平滑加权轮询
}

// WeightedRoundRobin 实现平滑加权轮询
type WeightedRoundRobin struct {
	items       []*WeightedItem // 所有待轮询的元素
	totalWeight int             // 所有元素的权重总和
}

// NewWeightedRoundRobin 用给定的元素初始化一个 WeightedRoundRobin
func NewWeightedRoundRobin(items []*WeightedItem) *WeightedRoundRobin {
	wrr := &WeightedRoundRobin{items: items}
	// 计算总权重
	for _, item := range items {
		wrr.totalWeight += item.Weight
	}
	return wrr
}

// Next 返回下一次要选中的元素
func (wrr *WeightedRoundRobin) Next() *WeightedItem {
	if len(wrr.items) == 0 {
		return nil
	}

	// 在循环开始前，selected 尚未指向任何元素，因此初始为 nil
	var selected *WeightedItem

	for _, item := range wrr.items {
		// 1. 先令每个 item 的 currentWeight += item.Weight
		//    这样能够让长时间未被选中的元素快速“补偿”权重，
		//    让它们有机会在下一次循环中脱颖而出
		item.currentWeight += item.Weight

		// 2. 判断是否需要更新 selected
		//    - 第一次循环，selected == nil 为真，selected 被赋值为第一个 item
		//    - 之后的循环，仅当当前 item 的 currentWeight > selected.currentWeight 时，
		//      才更新 selected，让 selected 始终指向 currentWeight 最大的元素
		if selected == nil || item.currentWeight > selected.currentWeight {
			selected = item
		}
	}

	// 3. 对被选中的元素减去总权重，以防止它在短期内再次获得过多的优势
	selected.currentWeight -= wrr.totalWeight

	return selected
}

func main() {
	// 准备一些测试数据
	items := []*WeightedItem{
		{Value: "A", Weight: 1},
		{Value: "B", Weight: 2},
		{Value: "C", Weight: 5},
	}

	// 初始化平滑加权轮询结构
	wrr := NewWeightedRoundRobin(items)

	// 模拟多次选取，统计每个元素被选中的次数
	count := make(map[string]int)
	for i := 0; i < 100; i++ {
		sel := wrr.Next()
		fmt.Print(sel.Value)
		count[sel.Value]++
	}

	// 打印分布结果
	fmt.Println("\nCount Distribution:", count)
}

// 输出结果
// CBCACCBCCBCACCBCCBCACCBCCBCACCBCCBCACCBCCBCACCBCCBCACCBCCBCACCBCCBCACCBCCBCACCBCCBCACCBCCBCACCBCCBCA
// Count Distribution: map[A:13 B:25 C:62]

最小连接数负载均衡

package main

import (
	"container/list"
	"fmt"
	"math/rand"
	"sync"
	"time"
)

// Server 结构体
type Server struct {
	Address     string
	Connections int
}

// LoadBalancer 结构体
type LoadBalancer struct {
	servers        []*Server
	connectionMap  map[int]*list.List        // key: 连接数, value: 服务器链表
	serverNodes    map[*Server]*list.Element // 服务器到链表节点的映射
	minConnections int                       // 记录当前最小连接数
	mutex          sync.Mutex
}

// NewLoadBalancer 创建负载均衡器
func NewLoadBalancer(addresses []string) *LoadBalancer {
	lb := &LoadBalancer{
		servers:        make([]*Server, len(addresses)),
		connectionMap:  make(map[int]*list.List),
		serverNodes:    make(map[*Server]*list.Element),
		minConnections: 0,
	}

	for i, addr := range addresses {
		server := &Server{Address: addr, Connections: 0}
		lb.servers[i] = server

		// 初始化 connectionMap
		if lb.connectionMap[0] == nil {
			lb.connectionMap[0] = list.New()
		}
		lb.serverNodes[server] = lb.connectionMap[0].PushBack(server)
	}

	return lb
}

// GetLeastConnectionServer 获取最小连接数服务器
func (lb *LoadBalancer) GetLeastConnectionServer() *Server {
	lb.mutex.Lock()
	defer lb.mutex.Unlock()

	servers, exists := lb.connectionMap[lb.minConnections]
	if !exists || servers.Len() == 0 {
		return nil
	}

	element := servers.Front()
	server := element.Value.(*Server)

	fmt.Printf("Selected server: %s with %d connections\n", server.Address, server.Connections)

	lb.updateServerConnections(server, server.Connections+1)
	return server
}

// updateServerConnections 更新服务器连接数
func (lb *LoadBalancer) updateServerConnections(server *Server, newConnections int) {
	oldConnections := server.Connections
	server.Connections = newConnections

	if node, exists := lb.serverNodes[server]; exists {
		lb.connectionMap[oldConnections].Remove(node)
		if lb.connectionMap[oldConnections].Len() == 0 {
			delete(lb.connectionMap, oldConnections)

			// 更新 minConnections，确保不会一直选择相同的服务器
			if oldConnections == lb.minConnections {
				lb.minConnections = newConnections
				for conn := range lb.connectionMap {
					if conn < lb.minConnections {
						lb.minConnections = conn
					}
				}
			}
		}
	}

	if lb.connectionMap[newConnections] == nil {
		lb.connectionMap[newConnections] = list.New()
	}
	lb.serverNodes[server] = lb.connectionMap[newConnections].PushBack(server)
}

// ReleaseConnection 释放服务器连接
func (lb *LoadBalancer) ReleaseConnection(server *Server) {
	lb.mutex.Lock()
	defer lb.mutex.Unlock()
	fmt.Printf("Releasing connection on server: %s, current connections: %d\n", server.Address, server.Connections)
	lb.updateServerConnections(server, server.Connections-1)
}

// HandleRequest 处理请求
func (lb *LoadBalancer) HandleRequest() {
	server := lb.GetLeastConnectionServer()
	if server == nil {
		fmt.Println("No available servers")
		return
	}

	time.Sleep(time.Duration(rand.Intn(3)+1) * time.Second)
	lb.ReleaseConnection(server)
}

func main() {
	rand.Seed(time.Now().UnixNano())
	serverAddresses := []string{"192.168.1.1", "192.168.1.2", "192.168.1.3"}
	lb := NewLoadBalancer(serverAddresses)

	var wg sync.WaitGroup
	for i := 0; i < 50; i++ {
		wg.Add(1)
		go func() {
			defer wg.Done()
			lb.HandleRequest()
		}()
		time.Sleep(time.Millisecond * 500) // 避免所有请求瞬间涌入
	}

	wg.Wait()
}


// 输出结果
// Selected server: 192.168.1.1 with 0 connections
// Selected server: 192.168.1.2 with 0 connections
// Selected server: 192.168.1.3 with 0 connections
// Selected server: 192.168.1.1 with 1 connections
// Selected server: 192.168.1.2 with 1 connections
// Selected server: 192.168.1.3 with 1 connections
// Releasing connection on server: 192.168.1.2, current connections: 2
// Selected server: 192.168.1.1 with 2 connections
// Releasing connection on server: 192.168.1.2, current connections: 1
// Releasing connection on server: 192.168.1.1, current connections: 3
// Releasing connection on server: 192.168.1.3, current connections: 2
// Releasing connection on server: 192.168.1.1, current connections: 2
// Selected server: 192.168.1.2 with 0 connections
// Selected server: 192.168.1.3 with 1 connections
// Selected server: 192.168.1.1 with 1 connections
// Releasing connection on server: 192.168.1.3, current connections: 2
// Releasing connection on server: 192.168.1.1, current connections: 2
// Selected server: 192.168.1.2 with 1 connections
// Releasing connection on server: 192.168.1.1, current connections: 1
// Selected server: 192.168.1.3 with 1 connections
// Selected server: 192.168.1.1 with 0 connections
// Selected server: 192.168.1.1 with 1 connections
// Releasing connection on server: 192.168.1.2, current connections: 2
// Selected server: 192.168.1.3 with 2 connections
// Releasing connection on server: 192.168.1.3, current connections: 3
// Releasing connection on server: 192.168.1.2, current connections: 1
// Selected server: 192.168.1.1 with 2 connections
// Releasing connection on server: 192.168.1.3, current connections: 2
// Selected server: 192.168.1.2 with 0 connections
// Releasing connection on server: 192.168.1.3, current connections: 1
// Selected server: 192.168.1.2 with 1 connections
// Releasing connection on server: 192.168.1.1, current connections: 3
// Selected server: 192.168.1.3 with 0 connections
// Releasing connection on server: 192.168.1.1, current connections: 2
// Selected server: 192.168.1.3 with 1 connections
// Releasing connection on server: 192.168.1.1, current connections: 1
......

限流器

实现一个限流器，支持以下功能：

每秒最多允许 N 个请求通过。
如果请求超过限制，则拒绝请求或等待直到可以处理。

可以使用 time.Ticker 和 chan 来实现一个简单的限流器。

1. RateLimiter 结构体:
- rate: 每秒允许的请求数。
- bucket: 令牌桶，用于存放令牌。
- ticker: 定时器，用于定期生成令牌。
- stopChan: 用于停止限流器的信号。
1. NewRateLimiter 函数：创建一个新的限流器，并启动令牌生成器。
1. tokenGenerator 方法：定期生成令牌并放入令牌桶中。如果令牌桶已满，则丢弃令牌。
1. Allow 方法：检查是否允许请求通过。如果令牌桶中有令牌，则允许请求并返回 true，否则返回 false。
1. Wait 方法：等待直到令牌桶中有令牌，然后允许请求通过。
1. Stop 方法：停止限流器，停止令牌生成器。

package main

import (
	"fmt"
	"time"
)

// RateLimiter 限流器结构体
type RateLimiter struct {
	rate     int           // 每秒允许的请求数
	bucket   chan struct{} // 令牌桶
	ticker   *time.Ticker  // 定时器
	stopChan chan struct{} // 停止信号
}

// NewRateLimiter 创建一个新的限流器
func NewRateLimiter(rate int, size int) *RateLimiter {
	rl := &RateLimiter{
		rate:     rate,
		bucket:   make(chan struct{}, size),
		ticker:   time.NewTicker(time.Second / time.Duration(rate)), // 计算出每个令牌生成的时间间隔
		stopChan: make(chan struct{}),
	}

	// 预先填充令牌桶
	for i := 0; i < size; i++ {
		rl.bucket <- struct{}{}
	}

	// 启动令牌生成器
	go rl.tokenGenerator()

	return rl
}

// tokenGenerator 令牌生成器
func (rl *RateLimiter) tokenGenerator() {
	for {
		select {
		case <-rl.ticker.C:
			select {
			case rl.bucket <- struct{}{}:
				// 成功放入令牌
			default:
				// 令牌桶已满，丢弃令牌
			}
		case <-rl.stopChan:
			rl.ticker.Stop()
			return
		}
	}
}

// Allow 检查是否允许请求通过
func (rl *RateLimiter) Allow() bool {
	select {
	case <-rl.bucket:
		return true
	default:
		return false
	}
}

// Wait 等待直到可以处理请求
func (rl *RateLimiter) Wait() {
	<-rl.bucket
}

// Stop 停止限流器
func (rl *RateLimiter) Stop() {
	close(rl.stopChan)
}

func main() {
	// 创建一个每秒允许 2 个请求的限流器，令牌桶大小为 3
	rl := NewRateLimiter(2, 3)

	// 模拟请求
	for i := 1; i <= 5; i++ {
		if rl.Allow() {
			fmt.Printf("Request %d allowed\n", i)
		} else {
			fmt.Printf("Request %d denied\n", i)
		}
		time.Sleep(200 * time.Millisecond)
	}

	// 再次模拟请求
	for i := 6; i <= 10; i++ {
		rl.Wait()
		fmt.Printf("Request %d allowed after wait\n", i)
	}

	// 停止限流器
	rl.Stop()
}

// 输出结果
// Request 1 allowed
// Request 2 allowed
// Request 3 allowed
// Request 4 allowed
// Request 5 denied
// Request 6 allowed after wait
// Request 7 allowed after wait
// Request 8 allowed after wait
// Request 9 allowed after wait
// Request 10 allowed after wait

设计推特

设计一个简化版的推特(Twitter)，可以让用户实现发送推文，关注/取消关注其他用户，能够看见关注人（包括自己）的最近 10 条推文。

实现 Twitter 类：

Twitter() 初始化简易版推特对象
void postTweet(int userId, int tweetId) 根据给定的 tweetId 和 userId 创建一条新推文。每次调用此函数都会使用一个不同的 tweetId。
List<Integer> getNewsFeed(int userId) 检索当前用户新闻推送中最近 10 条推文的 ID 。新闻推送中的每一项都必须是由用户关注的人或者是用户自己发布的推文。推文必须按照时间顺序由最近到最远排序。
void follow(int followerId, int followeeId) ID 为 followerId 的用户开始关注 ID 为 followeeId 的用户。
void unfollow(int followerId, int followeeId) ID 为 followerId 的用户不再关注 ID 为 followeeId 的用户。

package main

import (
	"container/heap"
	"fmt"
)

// Twitter 结构体，模拟 Twitter 系统
type Twitter struct {
	timeStamp int                      // 全局时间戳，确保推文按时间顺序排列
	tweets    map[int][]Tweet          // 用户推文记录，key: 用户ID, value: 推文列表
	followees map[int]map[int]struct{} // 关注关系表，key: 用户ID, value: 关注的用户集合，followees 记录的是某个用户关注了哪些用户。
}

// Tweet 结构体，表示一条推文
type Tweet struct {
	id        int // 推文 ID
	timeStamp int // 发送时间戳
}

// TweetHeap 结构体，实现最小堆（按时间戳倒序）
type TweetHeap []Tweet

// 堆相关操作：实现 `heap.Interface`
func (h TweetHeap) Len() int           { return len(h) }
func (h TweetHeap) Less(i, j int) bool { return h[i].timeStamp > h[j].timeStamp } // 时间戳大的排前面
func (h TweetHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

// Push 操作，将新推文加入堆
func (h *TweetHeap) Push(x interface{}) {
	*h = append(*h, x.(Tweet))
}

// Pop 操作，从堆中弹出最旧的推文
func (h *TweetHeap) Pop() interface{} {
	old := *h
	n := len(old)
	tweet := old[n-1] // 取最后一个元素（时间最早的）
	*h = old[:n-1]
	return tweet
}

// 构造函数，初始化 Twitter
func Constructor() Twitter {
	return Twitter{
		tweets:    make(map[int][]Tweet),
		followees: make(map[int]map[int]struct{}),
	}
}

// PostTweet 让用户 `userId` 发送一条推文 `tweetId`
func (this *Twitter) PostTweet(userId int, tweetId int) {
	this.timeStamp++ // 递增时间戳，确保推文顺序
	this.tweets[userId] = append(this.tweets[userId], Tweet{id: tweetId, timeStamp: this.timeStamp})
}

// GetNewsFeed 获取用户 `userId` 的最新推文（包含自己和关注的用户）
func (this *Twitter) GetNewsFeed(userId int) []int {
	h := &TweetHeap{}
	heap.Init(h)

	// 获取用户 `userId` 关注的所有用户（包括自己）
	users := this.followees[userId]
	if users == nil {
		users = make(map[int]struct{}) // 防止 `nil map` 赋值 panic
	}
	users[userId] = struct{}{} // 自己的推文也要加入

	// 遍历所有关注的用户，获取他们最近的推文
	for user := range users {
		tweets := this.tweets[user] // 获取用户的推文
		if len(tweets) > 0 {
			// 获取关注的用户的所有的推文
			for i := len(tweets) - 1; i >= 0; i-- {
				heap.Push(h, tweets[i])
			}
		}
	}

	// 取出最新的 10 条推文
	var res []int
	for len(*h) > 0 && len(res) < 10 {
		res = append(res, heap.Pop(h).(Tweet).id)
	}
	return res
}

// Follow 让 `followerId` 关注 `followeeId`
func (this *Twitter) Follow(followerId int, followeeId int) {
	// 如果 `followerId` 还没有关注别人，初始化 map
	if _, exists := this.followees[followerId]; !exists {
		this.followees[followerId] = make(map[int]struct{})
	}
	this.followees[followerId][followeeId] = struct{}{} // 关注 `followeeId`
}

// Unfollow 让 `followerId` 取消关注 `followeeId`
func (this *Twitter) Unfollow(followerId int, followeeId int) {
	if _, exists := this.followees[followerId]; exists {
		delete(this.followees[followerId], followeeId) // 取消关注
	}
}

// 测试代码
func main() {
	twitter := Constructor()

	// 用户 1 发送推文 5
	twitter.PostTweet(1, 5)
	fmt.Println(twitter.GetNewsFeed(1)) // 输出: [5]

	// 用户 1 关注用户 2
	twitter.Follow(1, 2)

	// 用户 2 发送推文 6
	twitter.PostTweet(2, 6)
	fmt.Println(twitter.GetNewsFeed(1)) // 输出: [6, 5]

	// 用户 1 取消关注用户 2
	twitter.Unfollow(1, 2)
	fmt.Println(twitter.GetNewsFeed(1)) // 输出: [5]
}

我的日程安排表 I

实现一个 MyCalendar 类来存放你的日程安排。如果要添加的日程安排不会造成重复预订，则可以存储这个新的日程安排。

当两个日程安排有一些时间上的交叉时（例如两个日程安排都在同一时间内），就会产生重复预订。

日程可以用一对整数 startTime 和 endTime 表示，这里的时间是半开区间，即 [startTime, endTime), 实数 x 的范围为，startTime <= x < endTime。

实现 MyCalendar 类：

MyCalendar() 初始化日历对象。
boolean book(int startTime, int endTime) 如果可以将日程安排成功添加到日历中而不会导致重复预订，返回 true。否则，返回 false 并且不要将该日程安排添加到日历中。

示例：

输入：
["MyCalendar", "book", "book", "book"]
[[], [10, 20], [15, 25], [20, 30]]
输出：
[null, true, false, true]

解释：
MyCalendar myCalendar = new MyCalendar();
myCalendar.book(10, 20); // return True
myCalendar.book(15, 25); // return False ，这个日程安排不能添加到日历中，因为时间 15 已经被另一个日程安排预订了。
myCalendar.book(20, 30); // return True ，这个日程安排可以添加到日历中，因为第一个日程安排预订的每个时间都小于 20，且不包含时间 20。

思路

维护一个有序的预约列表 events，其中每个元素 [start, end] 代表一个预约的起止时间。
每次调用 Book(start, end) 时：
1. 使用二分查找（sort.Search） 找到新预约的插入位置 i，即第一个 c.events[i][0] >= end 的索引，确保 end 早于 i 之后的预约开始时间。
2. 检查是否与前一个预约重叠：如果 i > 0 且 c.events[i-1][1] > start，说明新预约与前一个预约时间有重叠，返回 false。
3. 插入新预约并重新排序：使用 append() 插入新预约，并通过 sort.Slice() 维持 events 按照 start 时间升序排列，确保后续查找的正确性。

type MyCalendar struct {
    // 存储日程的开始时间和结束时间
	events [][]int
}

func Constructor() MyCalendar {
	return MyCalendar{events: [][]int{}}
}

func (c *MyCalendar) Book(start, end int) bool {
	// 使用二分查找找到插入位置
    // sort.Search 的第一个参数是搜索的范围，第二个参数用于判断 i 是否满足条件
    // i 代表新预约 start, end 的潜在插入位置
	i := sort.Search(len(c.events), func(i int) bool {
        // 新预约的 end 时间需要比老预约的 start 时间早
		return c.events[i][0] >= end
	})

	// 检查与前一个预约是否重叠
    // 即前一个预约的结束时间是否大于当前预约的开始时间
	if i > 0 && c.events[i-1][1] > start {
		return false
	}

	// 插入新的预约
	c.events = append(c.events, []int{start, end})
    // 按照预约的 start 时间重新排序
	sort.Slice(c.events, func(i, j int) bool {
		return c.events[i][0] < c.events[j][0]
	})

	return true
}

最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。

示例 1:

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

借用一个辅助栈 minStack，用于存获取 stack 中最小值。算法流程：

push() 方法：每当 push() 新值进来时，如果小于等于 minStack 栈顶值，则一起 push() 到 minStack，即更新了栈顶最小值；
pop() 方法：判断将 pop() 出去的元素值是否是 minStack 栈顶元素值（即最小值），如果是则将 minStack 栈顶元素一起 pop()，这样可以保证 minStack 栈顶元素始终是 stack 中的最小值。
getMin()方法：返回 minStack 栈顶即可。

type MinStack struct {
    stack, minStack []int
}

func Constructor() MinStack {
    return MinStack{}
}

func (q *MinStack) Push(val int)  {
    q.stack = append(q.stack, val)
    // 当 minStack 为空或者 minStack 的栈顶元素小于 val 时，将 val 压入 minStack
    if len(q.minStack) == 0 || val <= q.minStack[len(q.minStack)-1] {
        q.minStack = append(q.minStack, val)
    }
}

func (q *MinStack) Pop()  {
    val := q.stack[len(q.stack)-1]
    q.stack = q.stack[:len(q.stack)-1]
    if len(q.minStack) > 0 && val == q.minStack[len(q.minStack)-1] {
        q.minStack = q.minStack[:len(q.minStack)-1]
    }
}

func (q *MinStack) Top() int {
    return q.stack[len(q.stack)-1]
}

func (q *MinStack) GetMin() int {
    if len(q.minStack) > 0 {
        return q.minStack[len(q.minStack)-1]
    }
    return 0
}

最大频率栈

设计一个类似堆栈的数据结构，将元素推入堆栈，并从堆栈中弹出出现频率最高的元素。

实现 FreqStack 类:

FreqStack() 构造一个空的堆栈。
void push(int val) 将一个整数 val 压入栈顶。
int pop() 删除并返回堆栈中出现频率最高的元素。

如果出现频率最高的元素不只一个，则移除并返回最接近栈顶的元素。

示例 1：

输入：
["FreqStack","push","push","push","push","push","push","pop","pop","pop","pop"],
[[],[5],[7],[5],[7],[4],[5],[],[],[],[]]
输出：[null,null,null,null,null,null,null,5,7,5,4]
解释：
FreqStack = new FreqStack();
freqStack.push (5);//堆栈为 [5]
freqStack.push (7);//堆栈是 [5,7]
freqStack.push (5);//堆栈是 [5,7,5]
freqStack.push (7);//堆栈是 [5,7,5,7]
freqStack.push (4);//堆栈是 [5,7,5,7,4]
freqStack.push (5);//堆栈是 [5,7,5,7,4,5]
freqStack.pop ();//返回 5 ，因为 5 出现频率最高。堆栈变成 [5,7,5,7,4]。
freqStack.pop ();//返回 7 ，因为 5 和 7 出现频率最高，但7最接近顶部。堆栈变成 [5,7,5,4]。
freqStack.pop ();//返回 5 ，因为 5 出现频率最高。堆栈变成 [5,7,4]。
freqStack.pop ();//返回 4 ，因为 4, 5 和 7 出现频率最高，但 4 是最接近顶部的。堆栈变成 [5,7]。

核心思路：利用哈希表 + 栈维护元素的频率，并优先弹出频率最高的元素。

数据结构：

freqToVals：存储元素 val 的出现频率。
freqToVals map[int][]int：存储每个频率对应的元素栈，[]int 中最后的元素就是该频率最接近栈顶的元素。
maxFreq：存储当前栈中最大频率值。

算法执行过程如下 GIF 所示：

type FreqStack struct {
    // 记录 FreqStack 中元素的最大频率
    maxFreq int
    // 记录 FreqStack 中每个 val 对应的出现频率，后文就称为 VF 表
    valToFreq map[int]int
    // 记录频率 freq 对应的 val 列表，后文就称为 FV 表
    freqToVals map[int][]int
}

func Constructor() FreqStack {
    return FreqStack{
        valToFreq:  make(map[int]int),
        freqToVals: make(map[int][]int),
    }
}

func (this *FreqStack) Push(val int) {
    // 修改 VF 表：val 对应的 freq 加一
    freq := this.valToFreq[val] + 1
    this.valToFreq[val] = freq
    // 修改 FV 表：在 freq 对应的列表加上 val
    this.freqToVals[freq] = append(this.freqToVals[freq], val)
    // 更新 maxFreq
    if freq > this.maxFreq {
        this.maxFreq = freq
    }
}

func (this *FreqStack) Pop() int {
    // 修改 FV 表：pop 出一个 maxFreq 对应的元素 v
    vals := this.freqToVals[this.maxFreq]
    v := vals[len(vals)-1]
    this.freqToVals[this.maxFreq] = vals[:len(vals)-1]
    // 修改 VF 表：v 对应的 freq 减一
    this.valToFreq[v]--
    // 更新 maxFreq
    if len(this.freqToVals[this.maxFreq]) == 0 {
        // 如果 maxFreq 对应的元素空了
        delete(this.freqToVals, this.maxFreq)
        this.maxFreq--
    }
    return v
}

窥视迭代器

请你在设计一个迭代器，在集成现有迭代器拥有的 hasNext 和 next 操作的基础上，还额外支持 peek 操作。

实现 PeekingIterator 类：

PeekingIterator(Iterator<int> nums) 使用指定整数迭代器 nums 初始化迭代器。
int next() 返回数组中的下一个元素，并将指针移动到下个元素处。
bool hasNext() 如果数组中存在下一个元素，返回 true；否则，返回 false。
int peek() 返回数组中的下一个元素，但不移动指针。

注意：每种语言可能有不同的构造函数和迭代器 Iterator，但均支持 int next() 和 boolean hasNext() 函数。

示例 1：

输入：
["PeekingIterator", "next", "peek", "next", "next", "hasNext"]
[[[1, 2, 3]], [], [], [], [], []]
输出：
[null, 1, 2, 2, 3, false]

解释：
PeekingIterator peekingIterator = new PeekingIterator([1, 2, 3]); // [1,2,3]
peekingIterator.next();    // 返回 1 ，指针移动到下一个元素 [1,2,3]
peekingIterator.peek();    // 返回 2 ，指针未发生移动 [1,2,3]
peekingIterator.next();    // 返回 2 ，指针移动到下一个元素 [1,2,3]
peekingIterator.next();    // 返回 3 ，指针移动到下一个元素 [1,2,3]
peekingIterator.hasNext(); // 返回 False

代码的核心思路是使用 _next 变量缓存 Iterator.next() 的结果，并用 _hasNext 变量记录 Iterator.hasNext() 的状态，从而实现 peek() 方法在不改变迭代器状态的情况下返回下一个元素。next() 方法则先返回 _next，然后检查 Iterator 是否还有下一个元素，并提前缓存，以确保 peek() 始终可用。

package main

import "fmt"

// 迭代器结构，模拟 LeetCode 的 Iterator
type Iterator struct {
	nums  []int // 存储要遍历的数组
	index int   // 当前索引位置
}

// hasNext 方法：判断是否还有下一个元素
func (it *Iterator) hasNext() bool {
	return it.index < len(it.nums)
}

// next 方法：返回当前元素，并将索引前移
func (it *Iterator) next() int {
	if it.hasNext() {
		val := it.nums[it.index]
		it.index++ // 移动索引
		return val
	}
	return -1 // 假设不会调用到这里
}

// PeekingIterator 结构体
type PeekingIterator struct {
	iter     *Iterator // 指向原始迭代器
	_hasNext bool      // 记录是否还有下一个元素
	_next    int       // 缓存下一个元素
}

// 构造函数：初始化 PeekingIterator
func Constructor(iter *Iterator) *PeekingIterator {
	return &PeekingIterator{iter, iter.hasNext(), iter.next()}
}

// peek 方法：返回下一个元素，但不移动迭代器
func (it *PeekingIterator) peek() int {
	return it._next // 直接返回缓存的下一个元素
}

// next 方法：返回当前缓存的 _next，并更新缓存
func (it *PeekingIterator) next() int {
	ret := it._next // 取出当前缓存的元素

	// 检查原始迭代器是否还有下一个元素
	it._hasNext = it.iter.hasNext()
	if it._hasNext {
		it._next = it.iter.next() // 预取下一个元素
	}

	return ret
}

// hasNext 方法：返回是否还有下一个元素
func (it *PeekingIterator) hasNext() bool {
	return it._hasNext
}

// 主函数测试
func main() {
	// 创建一个 Iterator，初始化数据
	iter := &Iterator{nums: []int{1, 2, 3}, index: 0}

	// 用 Iterator 构造 PeekingIterator
	peekIter := Constructor(iter)

	// 测试 peek 和 next 方法
	fmt.Println(peekIter.peek())    // 1 (peek 返回当前元素但不移动迭代器)
	fmt.Println(peekIter.next())    // 1 (next 返回当前元素并移动迭代器)
	fmt.Println(peekIter.peek())    // 2 (peek 继续返回下一个元素)
	fmt.Println(peekIter.next())    // 2 (next 返回 2，并继续移动)
	fmt.Println(peekIter.next())    // 3 (返回 3)
	fmt.Println(peekIter.hasNext()) // false (已经没有下一个元素)
}

设计前中后队列

请你设计一个队列，支持在前，中，后三个位置的 push 和 pop 操作。

请你完成 FrontMiddleBack 类：

FrontMiddleBack() 初始化队列。
void pushFront(int val) 将 val 添加到队列的最前面。
void pushMiddle(int val) 将 val 添加到队列的正中间。
void pushBack(int val) 将 val 添加到队里的最后面。
int popFront() 将最前面的元素从队列中删除并返回值，如果删除之前队列为空，那么返回 -1。
int popMiddle() 将正中间的元素从队列中删除并返回值，如果删除之前队列为空，那么返回 -1。
int popBack() 将最后面的元素从队列中删除并返回值，如果删除之前队列为空，那么返回 -1。

请注意当有两个中间位置的时候，选择靠前面的位置进行操作。比方说：

将 6 添加到 [1, 2, 3, 4, 5] 的中间位置，结果数组为 [1, 2, 6, 3, 4, 5]。从 [1, 2, 3, 4, 5, 6] 的中间位置弹出元素，返回 3 ，数组变为 [1, 2, 4, 5, 6]。

示例 1：

输入：
["FrontMiddleBackQueue", "pushFront", "pushBack", "pushMiddle", "pushMiddle", "popFront", "popMiddle", "popMiddle", "popBack", "popFront"]
[[], [1], [2], [3], [4], [], [], [], [], []]
输出：
[null, null, null, null, null, 1, 3, 4, 2, -1]

解释：
FrontMiddleBackQueue q = new FrontMiddleBackQueue();
q.pushFront(1);   // [1]
q.pushBack(2);    // [1, 2]
q.pushMiddle(3);  // [1, 3, 2]
q.pushMiddle(4);  // [1, 4, 3, 2]
q.popFront();     // 返回 1 -> [4, 3, 2]
q.popMiddle();    // 返回 3 -> [4, 2]
q.popMiddle();    // 返回 4 -> [2]
q.popBack();      // 返回 2 -> []
q.popFront();     // 返回 -1 -> [] （队列为空）

核心思路

采用双链表 left 和 right 存储队列元素：
- left 存储左半部分，right 存储右半部分。
- 右边的元素数量始终大于或等于左边，即：
  - 奇数个元素时：right 比 left 多一个。
  - 偶数个元素时：left 和 right 长度相等。
- 这样便于从中间插入或删除元素。
插入逻辑
- PushFront(val)：在 left 插入，插入后平衡队列。
- PushMiddle(val)：
  - 偶数元素：插入 right 头部。
  - 奇数元素：插入 left 尾部。
- PushBack(val)：在 right 插入，插入后平衡队列。
删除逻辑
- PopFront()：
  - 仅 1 个元素：直接从 right 删除。
  - 多个元素：从 left 取出最前面的元素，并保持平衡。
- PopMiddle()：
  - 偶数元素：删除 left 尾部元素。
  - 奇数元素：删除 right 头部元素。
- PopBack()：直接从 right 删除，删除后平衡队列。
平衡 balance()
- 右边最多比左边多 1 个元素。
- 左边多了 → 把 left 的最后一个元素移动到 right 头部。
- 右边多了 2 个 → 把 right 的第一个元素移动到 left 末尾。

package main

import (
	"container/list"
	"fmt"
)

// FrontMiddleBackQueue 结构体，使用两个双向链表分别存储队列的左右两部分
type FrontMiddleBackQueue struct {
	left  *list.List // 存储左半部分的元素
	right *list.List // 存储右半部分的元素
}

// 维护左右部分的平衡关系，确保右边元素数始终 ≥ 左边元素数，且最多多一个
func (q *FrontMiddleBackQueue) balance() {
	// 右边最多比左边多一个元素
	if q.right.Len() > q.left.Len()+1 {
		// 右边比左边多 2 个，需要将 right 头部元素移动到 left 的尾部
		q.left.PushBack(q.right.Remove(q.right.Front()))
	}
	// 左边不能比右边多，若左边多了一个元素，需要将 left 尾部元素移动到 right 头部
	if q.left.Len() > q.right.Len() {
		q.right.PushFront(q.left.Remove(q.left.Back()))
	}
}

// 构造函数，初始化 FrontMiddleBackQueue
func Constructor() FrontMiddleBackQueue {
	return FrontMiddleBackQueue{
		left:  list.New(),
		right: list.New(),
	}
}

// PushFront 在队列最前面插入元素
func (q *FrontMiddleBackQueue) PushFront(val int) {
	q.left.PushFront(val) // 直接插入到 left 头部
	q.balance()           // 维护左右平衡
}

// PushMiddle 在队列的中间插入元素
func (q *FrontMiddleBackQueue) PushMiddle(val int) {
	// 判断当前元素个数是奇数还是偶数
	if (q.left.Len()+q.right.Len())%2 == 0 {
		// 如果当前元素个数为偶数，则插入到 right 头部
		q.right.PushFront(val)
	} else {
		// 如果当前元素个数为奇数，则插入到 left 尾部
		q.left.PushBack(val)
	}
	q.balance() // 维护左右平衡
}

// PushBack 在队列最后插入元素
func (q *FrontMiddleBackQueue) PushBack(val int) {
	q.right.PushBack(val) // 直接插入到 right 尾部
	q.balance()           // 维护左右平衡
}

// PopFront 移除并返回队列的最前面元素
func (q *FrontMiddleBackQueue) PopFront() int {
	if q.left.Len()+q.right.Len() == 0 {
		return -1 // 队列为空，返回 -1
	}
	if q.left.Len()+q.right.Len() == 1 {
		// 只有 1 个元素时，直接从 right 头部删除
		return q.right.Remove(q.right.Front()).(int)
	}
	// 删除 left 头部的元素
	e := q.left.Remove(q.left.Front()).(int)
	q.balance() // 维护左右平衡
	return e
}

// PopMiddle 移除并返回队列的中间元素
func (q *FrontMiddleBackQueue) PopMiddle() int {
	if q.left.Len()+q.right.Len() == 0 {
		return -1 // 队列为空，返回 -1
	}
	var e int
	if (q.left.Len()+q.right.Len())%2 == 0 {
		// 如果当前元素个数为偶数，则删除 left 的尾部元素
		e = q.left.Remove(q.left.Back()).(int)
	} else {
		// 如果当前元素个数为奇数，则删除 right 的头部元素
		e = q.right.Remove(q.right.Front()).(int)
	}
	q.balance() // 维护左右平衡
	return e
}

// PopBack 移除并返回队列的最后一个元素
func (q *FrontMiddleBackQueue) PopBack() int {
	if q.left.Len()+q.right.Len() == 0 {
		return -1 // 队列为空，返回 -1
	}
	// 直接删除 right 的尾部元素
	e := q.right.Remove(q.right.Back()).(int)
	q.balance() // 维护左右平衡
	return e
}

// Size 返回队列当前的大小
func (q *FrontMiddleBackQueue) Size() int {
	return q.left.Len() + q.right.Len()
}

// 测试代码
func main() {
	queue := Constructor()
	queue.PushFront(1)
	queue.PushMiddle(2)
	queue.PushBack(3)
	fmt.Println(queue.PopMiddle()) // 输出 2
	queue.PushMiddle(4)
	fmt.Println(queue.PopFront())  // 输出 1
	fmt.Println(queue.PopBack())   // 输出 3
	fmt.Println(queue.PopMiddle()) // 输出 4
	fmt.Println(queue.PopMiddle()) // 输出 -1（队列为空）
}

无法吃午餐的学生数量

学校的自助午餐提供圆形和方形的三明治，分别用数字 0 和 1 表示。所有学生站在一个队列里，每个学生要么喜欢圆形的要么喜欢方形的。餐厅里三明治的数量与学生的数量相同。所有三明治都放在一个栈里，每一轮：

如果队列最前面的学生喜欢栈顶的三明治，那么会拿走它并离开队列。
否则，这名学生会放弃这个三明治并回到队列的尾部。

这个过程会一直持续到队列里所有学生都不喜欢栈顶的三明治为止。

给你两个整数数组 students 和 sandwiches，其中 sandwiches[i] 是栈里面第 i 个三明治的类型（i = 0 是栈的顶部），students[j] 是初始队列里第 j 名学生对三明治的喜好（j = 0 是队列的最开始位置）。请你返回无法吃午餐的学生数量。

示例 1：

输入：students = [1,1,0,0], sandwiches = [0,1,0,1]
输出：0 
解释：
- 最前面的学生放弃最顶上的三明治，并回到队列的末尾，学生队列变为 students = [1,0,0,1]。
- 最前面的学生放弃最顶上的三明治，并回到队列的末尾，学生队列变为 students = [0,0,1,1]。
- 最前面的学生拿走最顶上的三明治，剩余学生队列为 students = [0,1,1]，三明治栈为 sandwiches = [1,0,1]。
- 最前面的学生放弃最顶上的三明治，并回到队列的末尾，学生队列变为 students = [1,1,0]。
- 最前面的学生拿走最顶上的三明治，剩余学生队列为 students = [1,0]，三明治栈为 sandwiches = [0,1]。
- 最前面的学生放弃最顶上的三明治，并回到队列的末尾，学生队列变为 students = [0,1]。
- 最前面的学生拿走最顶上的三明治，剩余学生队列为 students = [1]，三明治栈为 sandwiches = [1]。
- 最前面的学生拿走最顶上的三明治，剩余学生队列为 students = []，三明治栈为 sandwiches = []。
所以所有学生都有三明治吃。

核心观察：

不用模拟队列轮转！可以直接统计 0 和 1 的学生数量。
如果 所有剩下的学生都不喜欢当前三明治，那么他们永远无法吃到。

步骤

统计 students 中喜欢 0 和 1 的人数，存入 studentCount[0] 和 studentCount[1]。
遍历 sandwiches（从栈顶开始）：
- 如果当前三明治类型 t 还有学生喜欢，则 studentCount[t]--，表示拿走一个。
- 如果当前三明治 t 没有对应的学生，则后续所有三明治都无法被拿走，返回 studentCount[0] + studentCount[1]（即剩下的学生数）。
如果所有三明治都被拿走，返回 0（所有学生都吃到了）。

func countStudents(students []int, sandwiches []int) int {
    // studentCount[0 or 1] 分别代表吃 0 和吃 1的学生数量
    studentCount := make([]int, 2)
    for _, t := range students {
        studentCount[t]++
    }
    // 遍历三明治栈，若栈顶的三明治无法被取走，则剩下的人都吃不上了
    for _, t := range sandwiches {
        if studentCount[t] == 0 {
            // 两种喜好加起来就是剩下的学生数量
            return studentCount[0] + studentCount[1]
        }
        studentCount[t]--
    }
    return 0
}

按递增顺序显示卡牌

牌组中的每张卡牌都对应有一个唯一的整数。你可以按你想要的顺序对这套卡片进行排序。

最初，这些卡牌在牌组里是正面朝下的（即，未显示状态）。

现在，重复执行以下步骤，直到显示所有卡牌为止：

从牌组顶部抽一张牌，显示它，然后将其从牌组中移出。
如果牌组中仍有牌，则将下一张处于牌组顶部的牌放在牌组的底部。
如果仍有未显示的牌，那么返回步骤 1。否则，停止行动。
返回能以递增顺序显示卡牌的牌组顺序。

答案中的第一张牌被认为处于牌堆顶部。

示例：

输入：[17,13,11,2,3,5,7]
输出：[2,13,3,11,5,17,7]
解释：
我们得到的牌组顺序为 [17,13,11,2,3,5,7]（这个顺序不重要），然后将其重新排序。
重新排序后，牌组以 [2,13,3,11,5,17,7] 开始，其中 2 位于牌组的顶部。
我们显示 2，然后将 13 移到底部。牌组现在是 [3,11,5,17,7,13]。
我们显示 3，并将 11 移到底部。牌组现在是 [5,17,7,13,11]。
我们显示 5，然后将 17 移到底部。牌组现在是 [7,13,11,17]。
我们显示 7，并将 13 移到底部。牌组现在是 [11,17,13]。
我们显示 11，然后将 17 移到底部。牌组现在是 [13,17]。
我们展示 13，然后将 17 移到底部。牌组现在是 [17]。
我们显示 17。
由于所有卡片都是按递增顺序排列显示的，所以答案是正确的。

思路：使用队列模拟

排序 deck（升序）。
使用队列 queue 存储索引 0~n-1。
按规则遍历 deck：
- 取 queue 队头索引，并放入结果数组对应位置。
- 若 queue 仍有元素，则将 queue 队头移动到队尾。

func deckRevealedIncreasing(deck []int) []int {
	n := len(deck)
	// 1. 对 deck 进行升序排序
	sort.Ints(deck)

	// 2. 使用 queue 记录索引
	queue := list.New()
	for i := 0; i < n; i++ {
		queue.PushBack(i) // 初始化索引队列 [0, 1, 2, ..., n-1]
	}

	// 3. 结果数组
	res := make([]int, n)

	// 4. 按照规则放置元素
	for _, val := range deck {
		// 取出当前队列头部索引
		idx := queue.Remove(queue.Front()).(int)
		// 在结果数组对应位置放置元素
		res[idx] = val
		// 若队列仍有元素，则将头部元素移动到队尾
		if queue.Len() > 0 {
			queue.PushBack(queue.Remove(queue.Front()))
		}
	}

	return res
}

考场就座

在考场里，有 n 个座位排成一行，编号为 0 到 n - 1。

当学生进入考场后，他必须坐在离最近的人最远的座位上。如果有多个这样的座位，他会坐在编号最小的座位上。(另外，如果考场里没有人，那么学生就坐在 0 号座位上。)

设计一个模拟所述考场的类。实现 ExamRoom 类：

ExamRoom(int n) 用座位的数量 n 初始化考场对象。
int seat() 返回下一个学生将会入座的座位编号。
void leave(int p) 指定坐在座位 p 的学生将离开教室。保证座位 p 上会有一位学生。

示例 1：

输入：
["ExamRoom", "seat", "seat", "seat", "seat", "leave", "seat"]
[[10], [], [], [], [], [4], []]
输出：
[null, 0, 9, 4, 2, null, 5]
解释：
ExamRoom examRoom = new ExamRoom(10);
examRoom.seat(); // 返回 0，房间里没有人，学生坐在 0 号座位。
examRoom.seat(); // 返回 9，学生最后坐在 9 号座位。
examRoom.seat(); // 返回 4，学生最后坐在 4 号座位。
examRoom.seat(); // 返回 2，学生最后坐在 2 号座位。
examRoom.leave(4);
examRoom.seat(); // 返回 5，学生最后坐在 5 号座位。

主要逻辑：

数据结构
- N：考场总座位数，编号从 0 到 N-1。
- students：存储当前已入座学生的座位编号，始终保持升序。
入座逻辑 (Seat())
- 特殊情况：
  - 若当前没有学生，直接让第一个学生坐在 0 号座位。
- 寻找最优座位：
  - 边界检查：
    - 计算 0 号座位到第一个学生的距离，若最优，则选择 0 号座位。
    - 计算 N-1 号座位到最后一个学生的距离，若更优，则选择 N-1 号座位。
  - 中间最大间距：
    - 遍历 students 数组，寻找相邻已入座的学生之间的最大间距 (curr - prev) / 2，取最优位置 prev + dist。
- 插入新座位
  - 新的座位加入 students 列表，并保持有序（使用 sort.Ints()）。
离座逻辑 (Leave(p))
- 通过 sort.SearchInts() 二分查找找到 p 在 students 列表中的索引。
- 通过切片操作 this.students = append(this.students[:idx], this.students[idx+1:]...) 删除该座位。

// ExamRoom 结构体
type ExamRoom struct {
	N        int    // 考场座位数
	students []int // 存储已坐下的学生的座位编号（升序）
}

// 构造函数
func Constructor(N int) ExamRoom {
	return ExamRoom{N: N, students: []int{}}
}

// 学生入座
func (this *ExamRoom) Seat() int {
	if len(this.students) == 0 {
		this.students = append(this.students, 0) // 第一个学生坐在 0 号座位
		return 0
	}

	
	// 找到最大间距的座位
	// 检查 0 号位置是否更优
	maxDist := this.students[0]
	pos := 0

    // 检查 N-1 是否更优
	lastSeat := this.N - 1
	if lastSeat-this.students[len(this.students)-1] > maxDist {
		pos = lastSeat
	}

	// 遍历 students 数组，找到最佳座位
	for i := 0; i < len(this.students)-1; i++ {
		prev, curr := this.students[i], this.students[i+1]
		dist := (curr - prev) / 2
		if dist > maxDist {
			maxDist = dist
			pos = prev + dist
		}
	}
	
	// 插入学生位置到有序数组
	this.students = append(this.students, pos)
	sort.Ints(this.students) // 保持升序

	return pos
}

// 学生离开
func (this *ExamRoom) Leave(p int) {
	// 在 students 数组中删除 p
	// sort.SearchInts 是 Go 语言标准库 sort 包中的二分查找方法，用于 在有序整数切片 []int 中查找目标值
	idx := sort.SearchInts(this.students, p)
	// 在 students 切片中删除元素 p
	this.students = append(this.students[:idx], this.students[idx+1:]...)
}

设计哈希映射

不使用任何内建的哈希表库设计一个哈希映射（HashMap）。

实现 MyHashMap 类：

MyHashMap() 用空映射初始化对象
void put(int key, int value) 向 HashMap 插入一个键值对 (key, value) 。如果 key 已经存在于映射中，则更新其对应的值 value。
int get(int key) 返回特定的 key 所映射的 value；如果映射中不包含 key 的映射，返回 -1。
void remove(key) 如果映射中存在 key 的映射，则移除 key 和它所对应的 value。

示例：

输入：
["MyHashMap", "put", "put", "get", "get", "put", "get", "remove", "get"]
[[], [1, 1], [2, 2], [1], [3], [2, 1], [2], [2], [2]]
输出：
[null, null, null, 1, -1, null, 1, null, -1]

解释：
MyHashMap myHashMap = new MyHashMap();
myHashMap.put(1, 1); // myHashMap 现在为 [[1,1]]
myHashMap.put(2, 2); // myHashMap 现在为 [[1,1], [2,2]]
myHashMap.get(1);    // 返回 1 ，myHashMap 现在为 [[1,1], [2,2]]
myHashMap.get(3);    // 返回 -1（未找到），myHashMap 现在为 [[1,1], [2,2]]
myHashMap.put(2, 1); // myHashMap 现在为 [[1,1], [2,1]]（更新已有的值）
myHashMap.get(2);    // 返回 1 ，myHashMap 现在为 [[1,1], [2,1]]
myHashMap.remove(2); // 删除键为 2 的数据，myHashMap 现在为 [[1,1]]
myHashMap.get(2);    // 返回 -1（未找到），myHashMap 现在为 [[1,1]]

核心思路：

使用数组（[]list.List）作为哈希桶：
- 通过 hash(key) = key % base 计算哈希值，确定 key 存在哪个桶里。
- base = 769（一个质数），可以减少哈希冲突，使 key 均匀分布。
使用 Go 的 container/list 作为桶：
- 每个桶是一个 list.List（双向链表），可以存储多个键值对（entry）。
- 采用 链地址法（Chaining） 处理哈希冲突，即当多个 key 映射到相同桶时，把它们存入链表。
插入 (Put)：
- 计算哈希值找到对应桶。
- 遍历桶（链表）查找 key：
  - 如果 key 已存在，更新其 value。
  - 如果 key 不存在，在链表尾部插入 entry{key, value}。
查询 (Get)：
- 计算哈希值找到对应桶。
- 遍历桶（链表）查找 key：
  - 如果找到 key，返回对应 value。
  - 如果找不到，返回 -1。
删除 (Remove)：
- 计算哈希值找到对应桶。
- 遍历桶（链表）查找 key：
  - 如果找到 key，删除该节点。

package main

import (
    "container/list"
)

const base = 769 // 质数 769 作为哈希表的桶数量，减少哈希冲突

// entry 结构体用于存储键值对
type entry struct {
    key, value int
}

// MyHashMap 结构体实现哈希映射
type MyHashMap struct {
    data []list.List // 使用 list.List 作为桶，每个桶是一个链表
}

// Constructor 初始化哈希表
func Constructor() MyHashMap {
    return MyHashMap{make([]list.List, base)} // 创建 base 个桶，每个桶是一个 list.List
}

// hash 计算哈希值，确定 key 应该存储在哪个桶
func (m *MyHashMap) hash(key int) int {
    return key % base
}

// Put 插入 (key, value) 到哈希表，如果 key 已存在，则更新值
func (m *MyHashMap) Put(key, value int) {
    h := m.hash(key) // 计算 key 的哈希值，找到对应桶
    // 遍历桶（链表）查看 key 是否已存在
    for e := m.data[h].Front(); e != nil; e = e.Next() {
        if et := e.Value.(entry); et.key == key { // 如果 key 已存在，则更新 value
            e.Value = entry{key, value}
            return
        }
    }
    // 如果 key 不存在，则添加新的键值对到链表尾部
    m.data[h].PushBack(entry{key, value})
}

// Get 获取 key 对应的 value，若 key 不存在返回 -1
func (m *MyHashMap) Get(key int) int {
    h := m.hash(key) // 计算 key 的哈希值
    // 遍历链表查找 key
    for e := m.data[h].Front(); e != nil; e = e.Next() {
        if et := e.Value.(entry); et.key == key {
            return et.value // 找到 key，返回对应的 value
        }
    }
    return -1 // key 不存在，返回 -1
}

// Remove 删除 key 对应的键值对
func (m *MyHashMap) Remove(key int) {
    h := m.hash(key) // 计算 key 的哈希值
    // 遍历链表查找 key
    for e := m.data[h].Front(); e != nil; e = e.Next() {
        if e.Value.(entry).key == key { // 找到 key，删除该节点
            m.data[h].Remove(e)
            return
        }
    }
}

带权随机选择 ​

平滑加权轮询 ​

最小连接数负载均衡 ​

限流器 ​

带权随机选择

平滑加权轮询

最小连接数负载均衡

限流器